H5. (a) Suppose A and B are similar matrices. Show that AK = 0 iff BK = 0, where k € N. (b) Find the characteristic polynomial of the matrix A4 given in H1. (c) Compute the companion matrix C of the polynomial found in (b). (d) Compute A42 and C². (e) Use (a) and (d) to show that A4 and C are NOT similar matrices. (H5(e) motivates using rational canonical form instead of C.) H6. Find the rational canonical form of each of the following matrices: (a) the matrix A4 given in H1 200 (b) 0 2 0 0 02 [2 1 07
H5. (a) Suppose A and B are similar matrices. Show that AK = 0 iff BK = 0, where k € N. (b) Find the characteristic polynomial of the matrix A4 given in H1. (c) Compute the companion matrix C of the polynomial found in (b). (d) Compute A42 and C². (e) Use (a) and (d) to show that A4 and C are NOT similar matrices. (H5(e) motivates using rational canonical form instead of C.) H6. Find the rational canonical form of each of the following matrices: (a) the matrix A4 given in H1 200 (b) 0 2 0 0 02 [2 1 07
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
H5 part d
![Log In
Sep
12
Read your lecture notes and do
Sec 2.3: 1 and
watch the 61-minute video on companion matrices and rational canonical form (use the link
provided or access it in the Modules section of our Canvas portal) and then do
H4. (a) Compute the companion matrix for the polynomial found in Question 2.3.1.
(b) Compute the companion matrix of the characteristic polynomial of the matrix given in
Question 2.1.11.
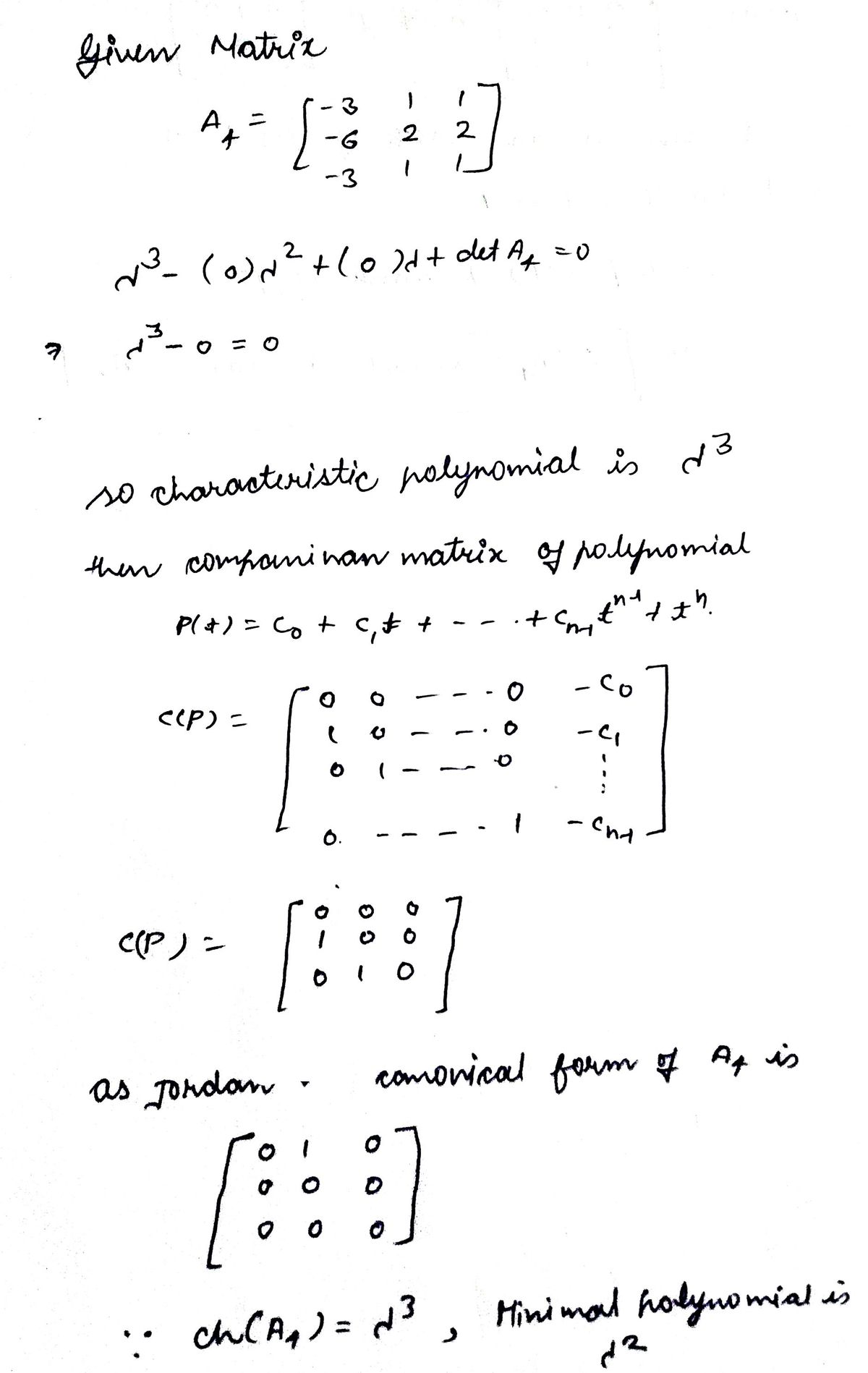
H5. (a) Suppose A and B are similar matrices. Show that AK = 0 iff Bk = 0, where k € N.
(b) Find the characteristic polynomial of the matrix A4 given in H1.
(c) Compute the companion matrix C of the polynomial found in (b).
(d) Compute A4² and C².
(e) Use (a) and (d) to show that A4 and C are NOT similar matrices.
(H5(e) motivates using rational canonical form instead of C.)
H6. Find the rational canonical form of each of the following matrices:
(a) the matrix A4 given in H1
[200]
(b) 0 2 0
0 02
[2 1 01](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2Fc074fc7e-4e48-46f1-bfc4-aee6ba4e6262%2F973613ce-5db2-41fe-84f3-6b5062557b40%2Fz2me58vs_processed.jpeg&w=3840&q=75)
Transcribed Image Text:Log In
Sep
12
Read your lecture notes and do
Sec 2.3: 1 and
watch the 61-minute video on companion matrices and rational canonical form (use the link
provided or access it in the Modules section of our Canvas portal) and then do
H4. (a) Compute the companion matrix for the polynomial found in Question 2.3.1.
(b) Compute the companion matrix of the characteristic polynomial of the matrix given in
Question 2.1.11.
H5. (a) Suppose A and B are similar matrices. Show that AK = 0 iff Bk = 0, where k € N.
(b) Find the characteristic polynomial of the matrix A4 given in H1.
(c) Compute the companion matrix C of the polynomial found in (b).
(d) Compute A4² and C².
(e) Use (a) and (d) to show that A4 and C are NOT similar matrices.
(H5(e) motivates using rational canonical form instead of C.)
H6. Find the rational canonical form of each of the following matrices:
(a) the matrix A4 given in H1
[200]
(b) 0 2 0
0 02
[2 1 01

Transcribed Image Text:29
Aug
31
|Recall that a scan of the instructor´s lecture notes from Fall 2021 can be accessed via ti
Modules section of our Canvas portal.
The information sheet for Quiz 1 is posted in Canvas.
Read your lecture notes and do
Sec 2.2: 2 (minimal polynomial part), and
H1. Repeat Questions 2.2.1 and 2.2.2 for the matrix A4, where
[-3 1 1
A4 = -6 22
-3 1 1
Sec 2.2: 3.
If any of the mathematics does not display properly (e.g., an error message received), o
with this file.
Expert Solution
Step 1
Step by step
Solved in 2 steps with 2 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

