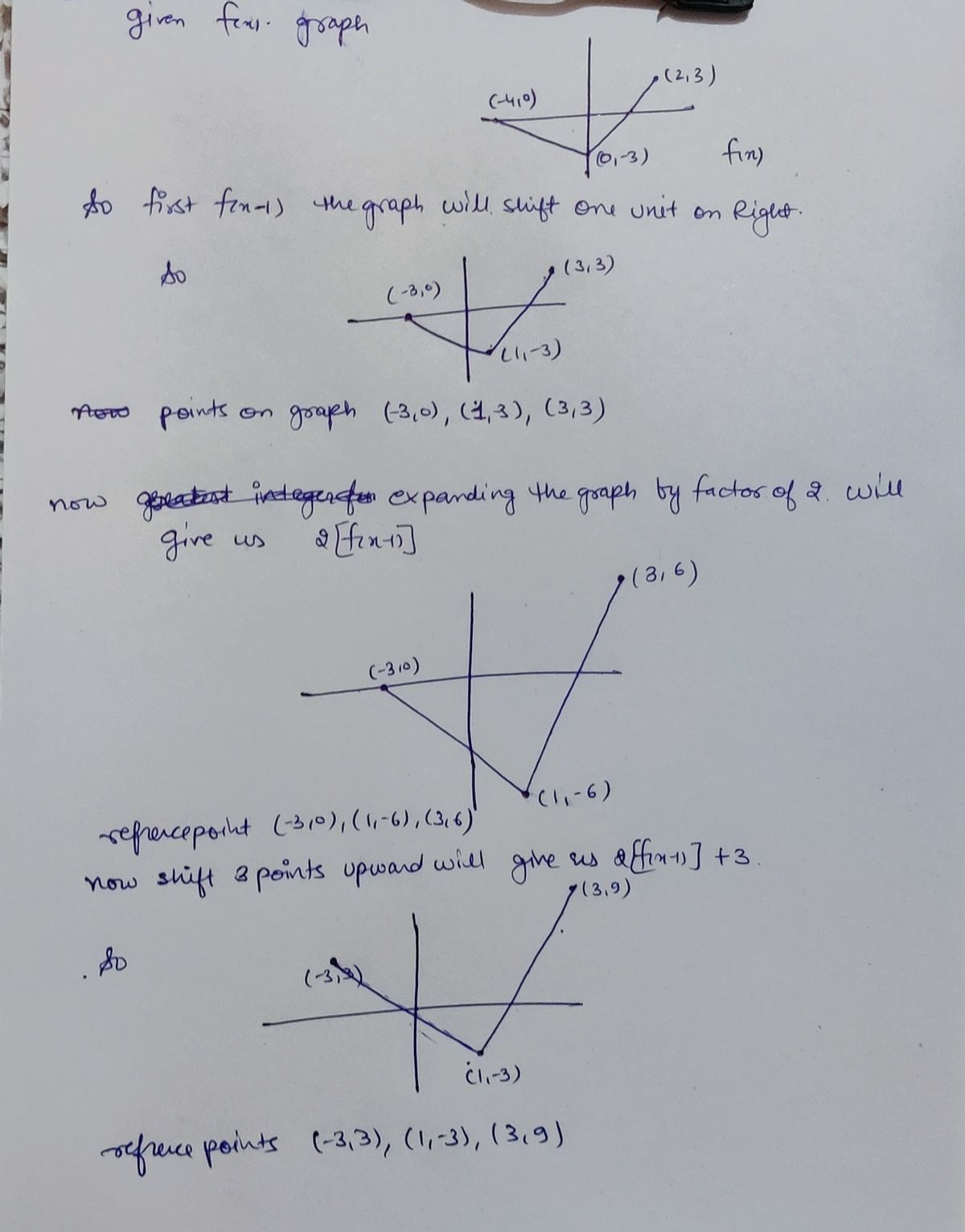
Graph the function y = 2[f(x - 1)] + 3 using transformations on basic function y = f(x) shown below. Draw each transformation to arrive at the final graph. Label each transformation graph and identify the reference points on each grid NOT next to the graph.
Graph the function y = 2[f(x - 1)] + 3 using transformations on basic function y = f(x) shown below. Draw each transformation to arrive at the final graph. Label each transformation graph and identify the reference points on each grid NOT next to the graph.
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
![### Graphing Transformations of a Function
**Task:** Graph the function \( y = 2[f(x - 1)] + 3 \) using transformations based on the basic function \( y = f(x) \) shown below. Complete each transformation step-by-step to arrive at the final graph.
**Instructions:**
1. **Draw each transformation** on a separate grid.
2. **Label each transformation graph** clearly.
3. **Identify the reference points** on each grid (not next to the graph).
**Given Points on the Graph:**
- (-4, 0)
- (0, -3)
- (2, 3)
**Graphs Provided:**
- **Initial Graph:** A grid with a basic V-shaped function defined by the points above.
- **Four Grids for Transformations:**
- Each labeled 1 to 4, these grids are provided for sketching transformations step-by-step.
**Transformation Explanation:**
- **Translation:**
- \( f(x - 1) \): Shift the graph of \( f(x) \) one unit to the right.
- **Vertical Scaling:**
- Multiply the function by 2: Stretches the graph vertically by a factor of 2.
- **Vertical Translation:**
- Add 3 to the function: Shift the entire graph up by 3 units.
By following the steps and labeling the points for each transformation on the grids provided, you will transform the initial V-shaped graph through the stages to achieve the final transformed graph.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F6b0cf1b8-84c6-4b32-890e-0885b2d3c430%2Fb1834c98-d25e-4721-9281-d28507acb1d0%2Fvus0jd_processed.jpeg&w=3840&q=75)
Transcribed Image Text:### Graphing Transformations of a Function
**Task:** Graph the function \( y = 2[f(x - 1)] + 3 \) using transformations based on the basic function \( y = f(x) \) shown below. Complete each transformation step-by-step to arrive at the final graph.
**Instructions:**
1. **Draw each transformation** on a separate grid.
2. **Label each transformation graph** clearly.
3. **Identify the reference points** on each grid (not next to the graph).
**Given Points on the Graph:**
- (-4, 0)
- (0, -3)
- (2, 3)
**Graphs Provided:**
- **Initial Graph:** A grid with a basic V-shaped function defined by the points above.
- **Four Grids for Transformations:**
- Each labeled 1 to 4, these grids are provided for sketching transformations step-by-step.
**Transformation Explanation:**
- **Translation:**
- \( f(x - 1) \): Shift the graph of \( f(x) \) one unit to the right.
- **Vertical Scaling:**
- Multiply the function by 2: Stretches the graph vertically by a factor of 2.
- **Vertical Translation:**
- Add 3 to the function: Shift the entire graph up by 3 units.
By following the steps and labeling the points for each transformation on the grids provided, you will transform the initial V-shaped graph through the stages to achieve the final transformed graph.
Expert Solution
Step 1
Step by step
Solved in 2 steps with 1 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

