Given X and Y are independent events respectively. P (X) = 0.65, P (Y) = 0.15. Event Z refers to the event that none of the events X and Y occurs. Event W refers to the event that if and only if one of the events X and Y occurs. (a) Find the probability P (Z), P (W), P (XW), P (X | Wc) respectively. (b) Are Z and W independent? Justify your answer (c) P(O) = 0.3, P(P) = a and P(O U P) = 0.7. Find the value of a if event O and P are independent.
Given X and Y are independent events respectively. P (X) = 0.65, P (Y) = 0.15. Event Z refers to the event that none of the events X and Y occurs. Event W refers to the event that if and only if one of the events X and Y occurs. (a) Find the probability P (Z), P (W), P (XW), P (X | Wc) respectively. (b) Are Z and W independent? Justify your answer (c) P(O) = 0.3, P(P) = a and P(O U P) = 0.7. Find the value of a if event O and P are independent.
A First Course in Probability (10th Edition)
10th Edition
ISBN:9780134753119
Author:Sheldon Ross
Publisher:Sheldon Ross
Chapter1: Combinatorial Analysis
Section: Chapter Questions
Problem 1.1P: a. How many different 7-place license plates are possible if the first 2 places are for letters and...
Related questions
Question

Transcribed Image Text:Given X and Y are independent events respectively. P (X) = 0.65,
P (Y) = 0.15. Event Z refers to the event that none of the events X and Y occurs. Event W
refers to the event that if and only if one of the events X and Y occurs.
(a) Find the probability P (Z), P (W), P (X | W), P (X | Wº) respectively.
(b) Are Z and W independent? Justify your answer
(c) P(O) = 0.3, P(P) = a and P(O U P) = 0.7. Find the value of a if event O and P
are independent.
(d) Assume event O and P are independent; event O and Q are independent; event P and Q
are
disjoint. Show that the events O and PUQ are independent.
(e) If Q.P and Q are events such that P (Q) > 0,
show that P(O U P |Q)=P(O | Q)+P( P | Q)—P(ON PIQ)
Expert Solution
Step 1
Dear students as per guidelines we solve only first three subparts only.
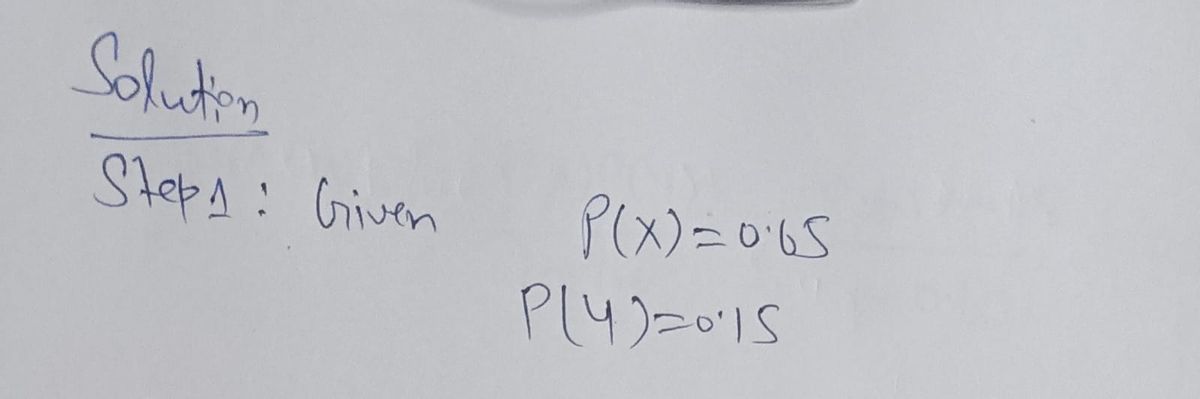
Step by step
Solved in 3 steps with 3 images

Recommended textbooks for you

A First Course in Probability (10th Edition)
Probability
ISBN:
9780134753119
Author:
Sheldon Ross
Publisher:
PEARSON


A First Course in Probability (10th Edition)
Probability
ISBN:
9780134753119
Author:
Sheldon Ross
Publisher:
PEARSON
