Given the line segment y =x,where 0< x < h a) Graph this line segment for 0 < x
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Topic Video
Question
Please do not skip steps
![### Line Segment and Volume of a Cone Example
Given the line segment \( y = \frac{a}{h} x \), where \( 0 \leq x \leq h \)
#### Part (a) Graph the Line Segment
Graph this line segment for \( 0 \leq x \leq h \) in the space below:
```
y-axis
| .
| /
| /
| /
| /
|/__________________ x-axis
```
#### Part (b) Rotation to Generate a Cone
Rotate this line segment about the x-axis will generate the cone with length \( h \) and radius of \( a \).
Use any integral method to show that the volume of this cone is:
\[ V = \frac{\pi}{3} h a^2 \]
(Note: This is the volume formula of a cone.)
**Instruction:** Must work the integral out by hand and show all steps.
---
### Detailed Explanation of the Integral Process
To find the volume of the cone by rotating the line segment \( y = \frac{a}{h} x \) around the x-axis, we use the disk method. Here's a step-by-step explanation:
1. **Set Up the Integral:**
Each disk's radius \( y \) is given by \( y = \frac{a}{h} x \). The volume \( V \) of the cone can be computed by integrating the area of these disks along the x-axis from 0 to \( h \):
\[
V = \pi \int_0^h \left(\frac{a}{h}x\right)^2 dx
\]
2. **Simplify the Integral:**
Substitute \( y = \frac{a}{h} x \):
\[
V = \pi \int_0^h \left(\frac{a^2}{h^2} x^2\right) dx
\]
3. **Factor Out Constants:**
\[
V = \frac{\pi a^2}{h^2} \int_0^h x^2 dx
\]
4. **Integrate \( x^2 \):**
Use the power rule for integration:
\[
\int x^2 dx = \frac{x^3}{3}
\]
5. **Evaluate the Integral:**](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F99269e07-9031-4b41-ba3f-5f1d3d15b266%2F2e3526a9-ac24-44b3-8a11-e71cc7f1b009%2Fw7xy9mo.png&w=3840&q=75)
Transcribed Image Text:### Line Segment and Volume of a Cone Example
Given the line segment \( y = \frac{a}{h} x \), where \( 0 \leq x \leq h \)
#### Part (a) Graph the Line Segment
Graph this line segment for \( 0 \leq x \leq h \) in the space below:
```
y-axis
| .
| /
| /
| /
| /
|/__________________ x-axis
```
#### Part (b) Rotation to Generate a Cone
Rotate this line segment about the x-axis will generate the cone with length \( h \) and radius of \( a \).
Use any integral method to show that the volume of this cone is:
\[ V = \frac{\pi}{3} h a^2 \]
(Note: This is the volume formula of a cone.)
**Instruction:** Must work the integral out by hand and show all steps.
---
### Detailed Explanation of the Integral Process
To find the volume of the cone by rotating the line segment \( y = \frac{a}{h} x \) around the x-axis, we use the disk method. Here's a step-by-step explanation:
1. **Set Up the Integral:**
Each disk's radius \( y \) is given by \( y = \frac{a}{h} x \). The volume \( V \) of the cone can be computed by integrating the area of these disks along the x-axis from 0 to \( h \):
\[
V = \pi \int_0^h \left(\frac{a}{h}x\right)^2 dx
\]
2. **Simplify the Integral:**
Substitute \( y = \frac{a}{h} x \):
\[
V = \pi \int_0^h \left(\frac{a^2}{h^2} x^2\right) dx
\]
3. **Factor Out Constants:**
\[
V = \frac{\pi a^2}{h^2} \int_0^h x^2 dx
\]
4. **Integrate \( x^2 \):**
Use the power rule for integration:
\[
\int x^2 dx = \frac{x^3}{3}
\]
5. **Evaluate the Integral:**
Expert Solution
Step 1
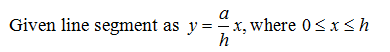
Step 2

Step by step
Solved in 3 steps with 3 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, advanced-math and related others by exploring similar questions and additional content below.Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

