Algebra and Trigonometry (6th Edition)
6th Edition
ISBN:9780134463216
Author:Robert F. Blitzer
Publisher:Robert F. Blitzer
ChapterP: Prerequisites: Fundamental Concepts Of Algebra
Section: Chapter Questions
Problem 1MCCP: In Exercises 1-25, simplify the given expression or perform the indicated operation (and simplify,...
Related questions
Question

Transcribed Image Text:**Problem:**
Given the function \( g(x) = 9 - x^2 \), evaluate \(\frac{g(x + h) - g(x)}{h}\), \( h \neq 0 \).
**Explanation:**
This problem asks you to find the difference quotient for the given function. The difference quotient is a fundamental concept in calculus that represents the slope of the secant line between two points on the graph of a function, often used as a step toward finding the derivative.
1. **Function Information:**
- The function is \( g(x) = 9 - x^2 \).
2. **Difference Quotient:**
- It is expressed as \(\frac{g(x + h) - g(x)}{h}\).
- This formula is used to calculate the average rate of change of the function over a small interval \( h \).
3. **Objective:**
- Evaluate the expression to find how the function changes as \( x \) changes by a small amount \( h \), assuming \( h \neq 0 \).
This exercise helps illustrate how derivatives are calculated as \( h \) approaches zero.
Expert Solution
Step 1
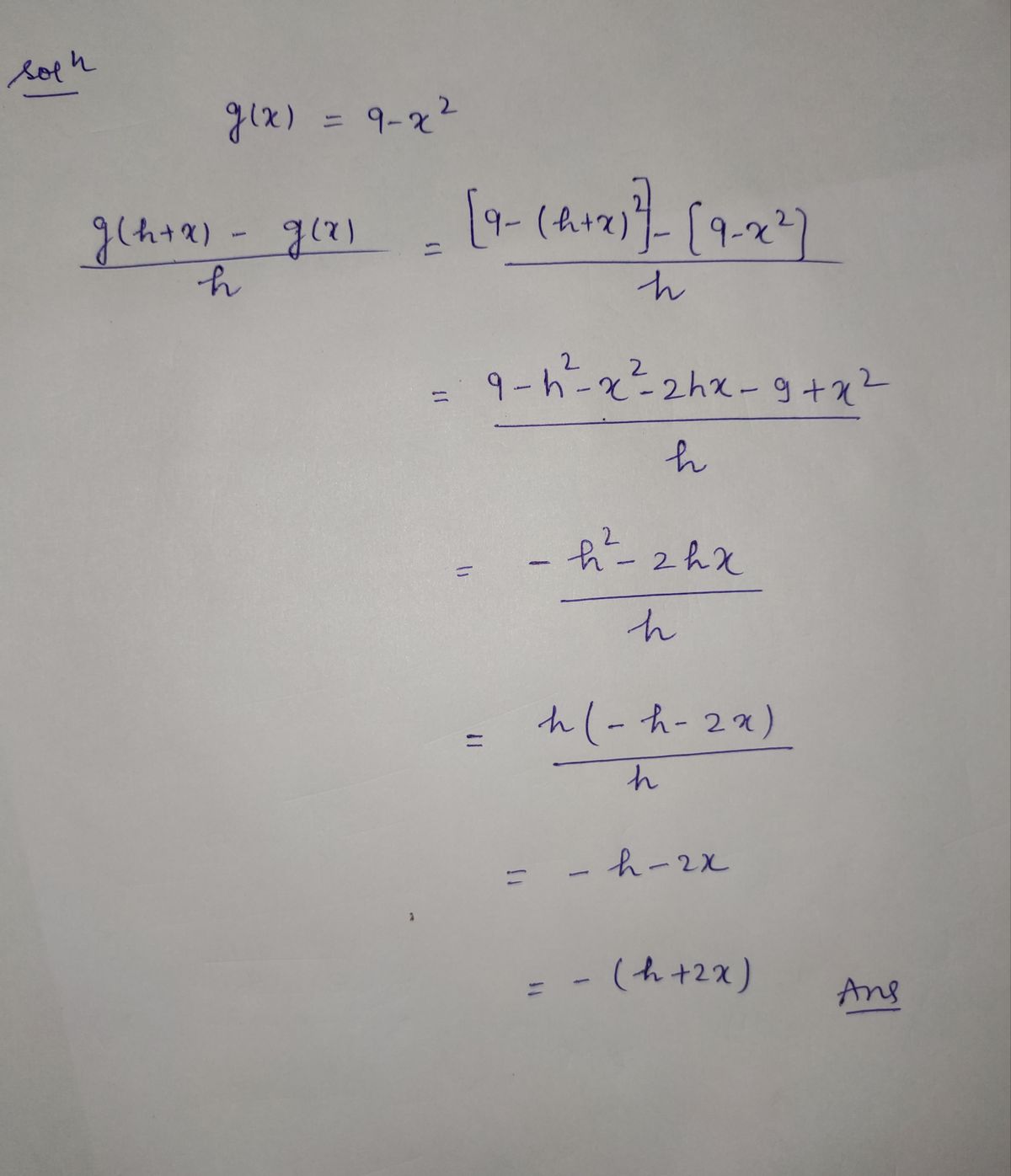
Step by step
Solved in 2 steps with 1 images

Recommended textbooks for you

Algebra and Trigonometry (6th Edition)
Algebra
ISBN:
9780134463216
Author:
Robert F. Blitzer
Publisher:
PEARSON

Contemporary Abstract Algebra
Algebra
ISBN:
9781305657960
Author:
Joseph Gallian
Publisher:
Cengage Learning

Linear Algebra: A Modern Introduction
Algebra
ISBN:
9781285463247
Author:
David Poole
Publisher:
Cengage Learning

Algebra and Trigonometry (6th Edition)
Algebra
ISBN:
9780134463216
Author:
Robert F. Blitzer
Publisher:
PEARSON

Contemporary Abstract Algebra
Algebra
ISBN:
9781305657960
Author:
Joseph Gallian
Publisher:
Cengage Learning

Linear Algebra: A Modern Introduction
Algebra
ISBN:
9781285463247
Author:
David Poole
Publisher:
Cengage Learning

Algebra And Trigonometry (11th Edition)
Algebra
ISBN:
9780135163078
Author:
Michael Sullivan
Publisher:
PEARSON

Introduction to Linear Algebra, Fifth Edition
Algebra
ISBN:
9780980232776
Author:
Gilbert Strang
Publisher:
Wellesley-Cambridge Press

College Algebra (Collegiate Math)
Algebra
ISBN:
9780077836344
Author:
Julie Miller, Donna Gerken
Publisher:
McGraw-Hill Education