GIVEN: P₂ = { a₁ + a₁x + a₂x² ao, a₁, a₂ ≤ R} T: P₂ R, T(a₁ + a₁x + a₂x²) = a₂ For example: 7(1- x + 3x²) = 3 PROVE: T is a linear transformation. -
GIVEN: P₂ = { a₁ + a₁x + a₂x² ao, a₁, a₂ ≤ R} T: P₂ R, T(a₁ + a₁x + a₂x²) = a₂ For example: 7(1- x + 3x²) = 3 PROVE: T is a linear transformation. -
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question

Transcribed Image Text:**Given:**
\( P_2 = \{ a_0 + a_1 x + a_2 x^2 \mid a_0, a_1, a_2 \in \mathbb{R} \} \)
**Transformation:**
\( T: P_2 \rightarrow \mathbb{R} \), where \( T(a_0 + a_1 x + a_2 x^2) = a_2 \).
*For example:* \( T(1 - x + 3x^2) = 3 \).
**Prove:** \( T \) is a linear transformation.
---
In the above content, \( P_2 \) is the space of all polynomials of degree at most 2 with real coefficients. The transformation \( T \) maps a quadratic polynomial to the coefficient of \( x^2 \).
To prove that \( T \) is a linear transformation, we need to show that it satisfies the properties of linearity:
1. **Additivity:** \( T(f + g) = T(f) + T(g) \) for any polynomials \( f, g \in P_2 \).
2. **Homogeneity:** \( T(c \cdot f) = c \cdot T(f) \) for any polynomial \( f \in P_2 \) and scalar \( c \in \mathbb{R} \).
Expert Solution
Step 1: Given
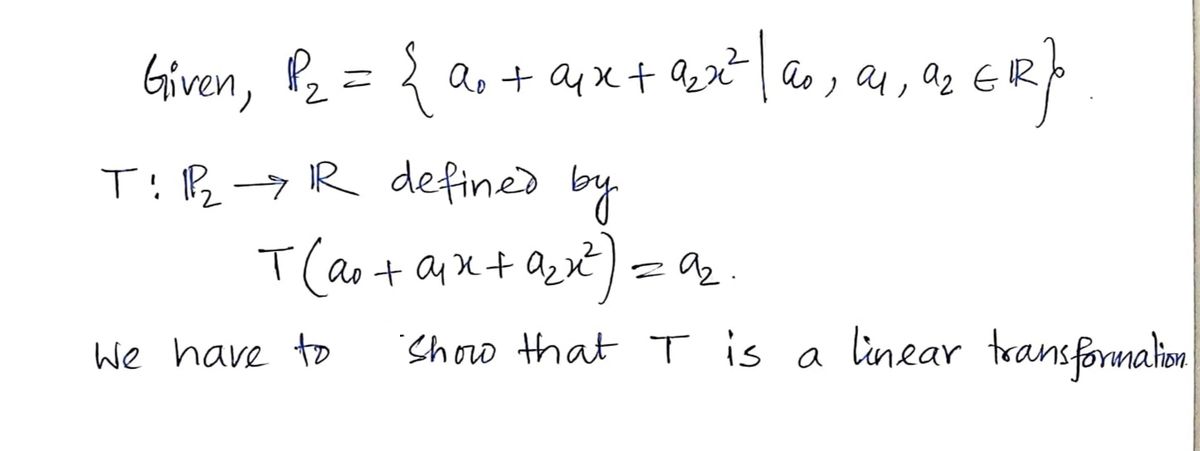
Step by step
Solved in 3 steps with 2 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

