Algebra and Trigonometry (6th Edition)
6th Edition
ISBN:9780134463216
Author:Robert F. Blitzer
Publisher:Robert F. Blitzer
ChapterP: Prerequisites: Fundamental Concepts Of Algebra
Section: Chapter Questions
Problem 1MCCP: In Exercises 1-25, simplify the given expression or perform the indicated operation (and simplify,...
Related questions
Question
![**Quadratic Equations and the Discriminant**
In this exercise, we are given a quadratic equation and instructed to determine the value of its discriminant. The equation provided is:
\[ X = 6 - 4X^2 \]
**Steps to Solve:**
1. **Rearrange the Equation**:
Convert the equation into the standard quadratic form \(ax^2 + bx + c = 0\).
\[ 4X^2 + X - 6 = 0 \]
2. **Identify Coefficients**:
- \(a = 4\)
- \(b = 1\)
- \(c = -6\)
3. **Calculate the Discriminant**:
The discriminant \(\Delta\) of a quadratic equation \(ax^2 + bx + c = 0\) is given by the formula:
\[ \Delta = b^2 - 4ac \]
Substitute the values of \(a\), \(b\), and \(c\) into the formula:
\[ \Delta = (1)^2 - 4(4)(-6) = 1 + 96 = 97 \]
**Conclusion**:
The discriminant of the quadratic equation \(4X^2 + X - 6 = 0\) is 97.
**Understanding the Discriminant**:
- A positive discriminant (\(\Delta > 0\)) indicates that the quadratic equation has two distinct real roots.
- If \(\Delta = 0\), the quadratic equation has exactly one real root (a repeated root).
- If \(\Delta < 0\), the quadratic equation has no real roots, but instead has two complex roots.
In this case, since \(\Delta = 97\) (which is positive), the quadratic equation has two distinct real roots.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2Ffbc91cea-da78-460b-a92b-33fe255237f9%2F2aede764-4d46-4660-9329-39c0067d8b23%2Fvm9poz8_processed.jpeg&w=3840&q=75)
Transcribed Image Text:**Quadratic Equations and the Discriminant**
In this exercise, we are given a quadratic equation and instructed to determine the value of its discriminant. The equation provided is:
\[ X = 6 - 4X^2 \]
**Steps to Solve:**
1. **Rearrange the Equation**:
Convert the equation into the standard quadratic form \(ax^2 + bx + c = 0\).
\[ 4X^2 + X - 6 = 0 \]
2. **Identify Coefficients**:
- \(a = 4\)
- \(b = 1\)
- \(c = -6\)
3. **Calculate the Discriminant**:
The discriminant \(\Delta\) of a quadratic equation \(ax^2 + bx + c = 0\) is given by the formula:
\[ \Delta = b^2 - 4ac \]
Substitute the values of \(a\), \(b\), and \(c\) into the formula:
\[ \Delta = (1)^2 - 4(4)(-6) = 1 + 96 = 97 \]
**Conclusion**:
The discriminant of the quadratic equation \(4X^2 + X - 6 = 0\) is 97.
**Understanding the Discriminant**:
- A positive discriminant (\(\Delta > 0\)) indicates that the quadratic equation has two distinct real roots.
- If \(\Delta = 0\), the quadratic equation has exactly one real root (a repeated root).
- If \(\Delta < 0\), the quadratic equation has no real roots, but instead has two complex roots.
In this case, since \(\Delta = 97\) (which is positive), the quadratic equation has two distinct real roots.
Expert Solution
Step 1: Given that
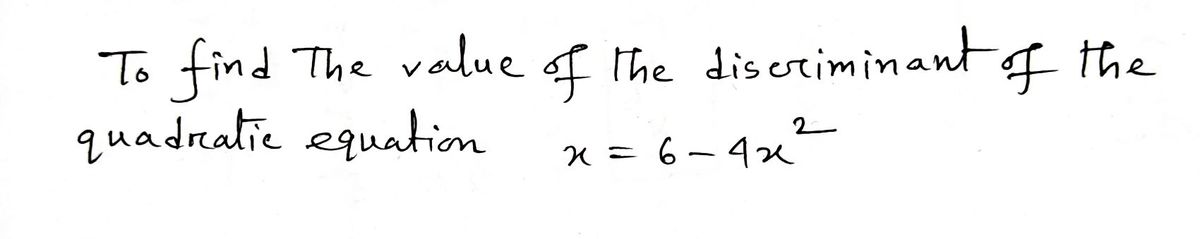
Step by step
Solved in 3 steps with 3 images

Recommended textbooks for you

Algebra and Trigonometry (6th Edition)
Algebra
ISBN:
9780134463216
Author:
Robert F. Blitzer
Publisher:
PEARSON

Contemporary Abstract Algebra
Algebra
ISBN:
9781305657960
Author:
Joseph Gallian
Publisher:
Cengage Learning

Linear Algebra: A Modern Introduction
Algebra
ISBN:
9781285463247
Author:
David Poole
Publisher:
Cengage Learning

Algebra and Trigonometry (6th Edition)
Algebra
ISBN:
9780134463216
Author:
Robert F. Blitzer
Publisher:
PEARSON

Contemporary Abstract Algebra
Algebra
ISBN:
9781305657960
Author:
Joseph Gallian
Publisher:
Cengage Learning

Linear Algebra: A Modern Introduction
Algebra
ISBN:
9781285463247
Author:
David Poole
Publisher:
Cengage Learning

Algebra And Trigonometry (11th Edition)
Algebra
ISBN:
9780135163078
Author:
Michael Sullivan
Publisher:
PEARSON

Introduction to Linear Algebra, Fifth Edition
Algebra
ISBN:
9780980232776
Author:
Gilbert Strang
Publisher:
Wellesley-Cambridge Press

College Algebra (Collegiate Math)
Algebra
ISBN:
9780077836344
Author:
Julie Miller, Donna Gerken
Publisher:
McGraw-Hill Education