Homework Help is Here – Start Your Trial Now!
Math
Advanced Math
Give an example of each of the following, or explain why no such example exists. (If you give an example, you do not need to provide any additional explanation; just give the example.) 1 1 1 (a) A matrix whose inverse is 22 2 3 3 3

Give an example of each of the following, or explain why no such example exists. (If you give an example, you do not need to provide any additional explanation; just give the example.) 1 1 1 (a) A matrix whose inverse is 22 2 3 3 3

Advanced Engineering Mathematics
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
See similar textbooks
icon
Related questions
Question
Give an example of each of the following, or explain why no such example exists. (If you give an example, you do not need to provide any additional explanation; just give the example.) 1 1 1 (a) A matrix whose inverse is 2 2 2 3 3 3 (b) The matrix for an onto linear transformation from R¹ to R³. (c) The matrix for a one-to-one linear transformation from R¹ to R³.
Transcribed Image Text:Give an example of each of the following, or explain why no such example exists. (If you give an example, you do not need to provide any additional explanation; just give the example.) 1 1 1 (a) A matrix whose inverse is 2 2 2 3 3 3 (b) The matrix for an onto linear transformation from R¹ to R³. (c) The matrix for a one-to-one linear transformation from R¹ to R³.
Expert Solution
Step 1

Since you have posted a multiple question according to guildlines I will solve first(a)   question for you. To get remaining part solved please repost the complete question and mention parts.

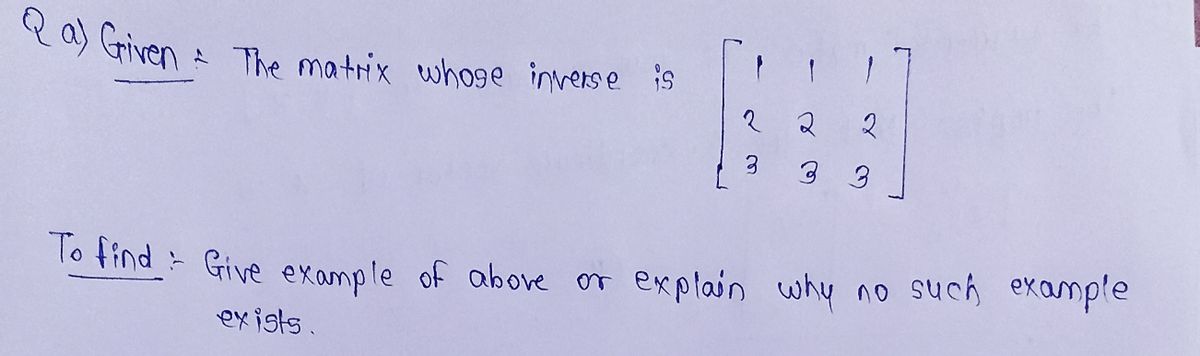
Advanced Math homework question answer, step 1, image 1

trending now

Trending now

This is a popular solution!

steps

Step by step

Solved in 2 steps with 2 images

SEE SOLUTIONCheck out a sample Q&A here
Blurred answer
Recommended textbooks for you
Advanced Engineering Mathematics
Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated
Numerical Methods for Engineers
Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education
Introductory Mathematics for Engineering Applicat…
Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY
Mathematics For Machine Technology
Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,
Basic Technical Mathematics
Basic Technical Mathematics
Advanced Math
ISBN:
9780134437705
Author:
Washington
Publisher:
PEARSON
Topology
Topology
Advanced Math
ISBN:
9780134689517
Author:
Munkres, James R.
Publisher:
Pearson,
SEE MORE TEXTBOOKS