Geochemical Box Models - please use same terminology found in question Consider an element X exchanging between two geochemical reservoirs A and B. Let MA and MB be the masses of X in reservoirs A and B, respectively; let tA and tB be the residence times of X in reservoirs A and B, respectively. Further let M = MA + MB be the total mass of X in the two reservoirs combined. Consider a situation where additional mass M' is injected into reservoir A at time t=0 increasing the total amount of element X in the system from M0 to M1, with no further injection at later times; further assume that tA >> tB, that the total mass in the altered system is M1 = M0 + M', and that M0 << M'. Give an expression for MB(t) as a function of M1, tA, tB, and t. What is the characteristic time for MB to approach steady state? What is the characteristic time for MA to approach steady state?
Geochemical Box Models - please use same terminology found in question
Consider an element X exchanging between two geochemical reservoirs A and B. Let MA and MB be the masses of X in reservoirs A and B, respectively; let tA and tB be the residence times of X in reservoirs A and B, respectively. Further let M = MA + MB be the total mass of X in the two reservoirs combined.
Consider a situation where additional mass M' is injected into reservoir A at time t=0 increasing the total amount of element X in the system from M0 to M1, with no further injection at later times; further assume that tA >> tB, that the total mass in the altered system is M1 = M0 + M', and that M0 << M'. Give an expression for MB(t) as a function of M1, tA, tB, and t. What is the characteristic time for MB to approach steady state? What is the characteristic time for MA to approach steady state?
First of all, write the net flux value,
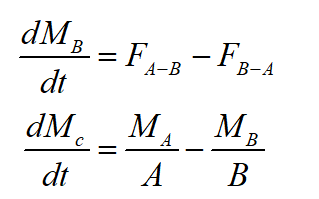
As, it is known that if CA>>CB,
Then MA is equivalent to M, so in this case substitute ‘n’ for the MA in the above equation,
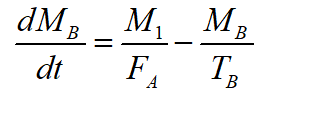
Trending now
This is a popular solution!
Step by step
Solved in 3 steps with 5 images









