Franz Beckenbauer and Johan Cruyff are purchasing managers for the headquarters of a large sports marketing company chain with a central inventory operation. Their fastest-moving inventory item has a daily demand of 35 units. The cost of each unit is £200, and the inventory carrying cost is £25 per unit per year. The average ordering cost is £60 per order. It takes about 5 days for an order to arrive, and there are 252 working days per year. a) To minimize the cost, how many units should be ordered each time an order is placed? What is the total annual inventory cost, including the cost of the units? b) How can they manage the days it takes for an order to arrive? (How does it impact their operations and costs?) c) b) Even if there is substantial uncertainty in the parameters in the EOQ-model, it is still quite a useful model. Discuss why.
Franz Beckenbauer and Johan Cruyff are purchasing managers for the headquarters of a large
sports marketing company chain with a central inventory operation. Their fastest-moving inventory item has
a daily demand of 35 units. The cost of each unit is £200, and the inventory carrying cost is £25 per unit
per year. The average ordering cost is £60 per order. It takes about 5 days for an order to arrive, and there
are 252 working days per year.
a) To minimize the cost, how many units should be ordered each time an order is placed?
What is the total annual inventory cost, including the cost of the units?
b) How can they manage the days it takes for an order to arrive? (How does it impact their
operations and costs?)
c) b) Even if there is substantial uncertainty in the parameters in the EOQ-model, it is still quite a
useful model. Discuss why.
I got this anwsers but i am not sure if its correct:
For question 1:
EOQ=294
Annual Holding Cost= Q/2 H= 2942×25=£3675
Annual Ordering Cost=Q/D S= 29435×252×60=£514.29
Annual Purchase Cost=D×P=35×252×200=£1,764,000
Purchase Cost=D×P=35×252×200=£1,764,000
Total Annual Cost=Annual Holding Cost+Annual Ordering Cost+Annual Purchase Cost=£1,769,189.29
For question 2:
Reorder Point (ROP)=Demand per day×Lead time=35×5=175
This indicates that the company should reorder when the inventory level reaches 175 units.
this is my first answer and my second with different answer is working out in pictuers but my answer down here:
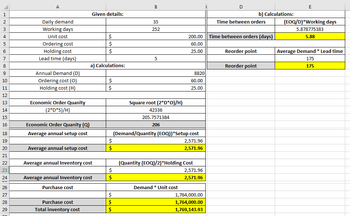
Ans 1.
| EOQ | 205.7571384 |
| Annual holding cost | 2571.96423 |
| Annual ordering cost | 2571.96423 |
| Annual purchase cost | 1764000 |
| Total annual cost | 1769143.93 |
Ans 2.
| Time between orders | 5.878775383 |


Trending now
This is a popular solution!
Step by step
Solved in 4 steps with 3 images

I understand what you wrote but i am not sure how to answer this questions about this:
for the first question 3A i am not sure if i should also include the graphs that are given to me when i asked the first question.
3A. To minimize the cost, how many units should be ordered each time an order is placed? What is the total annual inventory cost, including the cost of the units?
This question needs a quantitative approach.
First: Write clearly ALL the calculations STEP by STEP.
Second: Explain the process followed and the final result.
3B. How can they manage the days it takes for an order to arrive? (How does it impact their operations and costs?)
3C. Even if there is substantial uncertainty in the parameters in the EOQ-model, it is still quite a useful model. Discuss why.