Forted Withe 8.4.13 Let x = 4 sin 0 so that dr = 4 cos 0 d0. Note that V16- 1² = 4 cos 0. Thus, 1 4 cos e 4 cos e ()+c. dx = de = 0 +C = sin-1 16
Forted Withe 8.4.13 Let x = 4 sin 0 so that dr = 4 cos 0 d0. Note that V16- 1² = 4 cos 0. Thus, 1 4 cos e 4 cos e ()+c. dx = de = 0 +C = sin-1 16
Calculus: Early Transcendentals
8th Edition
ISBN:9781285741550
Author:James Stewart
Publisher:James Stewart
Chapter1: Functions And Models
Section: Chapter Questions
Problem 1RCC: (a) What is a function? What are its domain and range? (b) What is the graph of a function? (c) How...
Related questions
Question
No need to show all work here, I understand where we got theta+C. What I don't understand is how that equals sin^-1(x/4)? Where did this come from and how does it relate to theta + C?
![**Integration Exercise Example**
**Problem:**
Evaluate the integral:
\[
\int \frac{dx}{\sqrt{16 - x^2}}
\]
**Solution:**
1. **Substitution:**
Let \( x = 4 \sin \theta \), so that \( dx = 4 \cos \theta \, d\theta \).
2. **Simplification:**
Note that:
\[
\sqrt{16 - x^2} = \sqrt{16 - (4 \sin \theta)^2} = \sqrt{16(1 - \sin^2 \theta)} = \sqrt{16 \cos^2 \theta} = 4 \cos \theta
\]
3. **Integral Transformation:**
Rewrite the integral as:
\[
\int \frac{1}{\sqrt{16 - x^2}} \, dx = \int \frac{4 \cos \theta}{4 \cos \theta} \, d\theta = \int d\theta
\]
4. **Integration:**
\[
= \theta + C
\]
5. **Back-Substitute:**
Since \( \theta = \sin^{-1} \left(\frac{x}{4}\right) \), we have:
\[
\theta + C = \sin^{-1} \left(\frac{x}{4}\right) + C
\]
Thus, the solution to the integral is:
\[
\int \frac{dx}{\sqrt{16 - x^2}} = \sin^{-1} \left(\frac{x}{4}\right) + C
\]
**Notes:**
- This solution uses trigonometric substitution to evaluate the integral.
- The derivative and back-substitution steps ensure the solution is in terms of \( x \).](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F61b75115-d70f-4fe2-af93-2076876ad69a%2F6975774f-5803-4115-891e-a6afadd533b4%2Fyy4ddq9_processed.jpeg&w=3840&q=75)
Transcribed Image Text:**Integration Exercise Example**
**Problem:**
Evaluate the integral:
\[
\int \frac{dx}{\sqrt{16 - x^2}}
\]
**Solution:**
1. **Substitution:**
Let \( x = 4 \sin \theta \), so that \( dx = 4 \cos \theta \, d\theta \).
2. **Simplification:**
Note that:
\[
\sqrt{16 - x^2} = \sqrt{16 - (4 \sin \theta)^2} = \sqrt{16(1 - \sin^2 \theta)} = \sqrt{16 \cos^2 \theta} = 4 \cos \theta
\]
3. **Integral Transformation:**
Rewrite the integral as:
\[
\int \frac{1}{\sqrt{16 - x^2}} \, dx = \int \frac{4 \cos \theta}{4 \cos \theta} \, d\theta = \int d\theta
\]
4. **Integration:**
\[
= \theta + C
\]
5. **Back-Substitute:**
Since \( \theta = \sin^{-1} \left(\frac{x}{4}\right) \), we have:
\[
\theta + C = \sin^{-1} \left(\frac{x}{4}\right) + C
\]
Thus, the solution to the integral is:
\[
\int \frac{dx}{\sqrt{16 - x^2}} = \sin^{-1} \left(\frac{x}{4}\right) + C
\]
**Notes:**
- This solution uses trigonometric substitution to evaluate the integral.
- The derivative and back-substitution steps ensure the solution is in terms of \( x \).
Expert Solution
Step 1
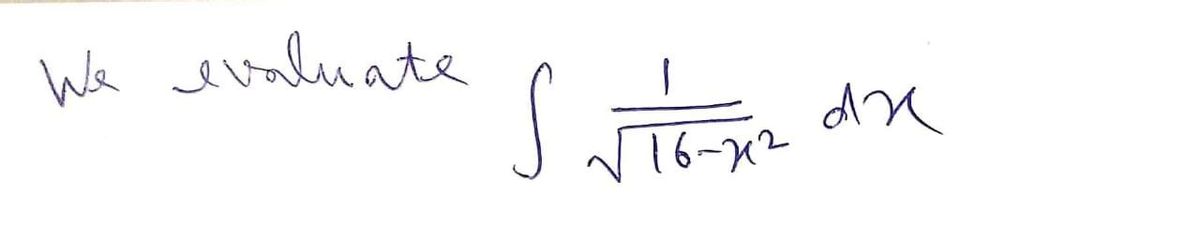
Step by step
Solved in 2 steps with 2 images

Recommended textbooks for you

Calculus: Early Transcendentals
Calculus
ISBN:
9781285741550
Author:
James Stewart
Publisher:
Cengage Learning

Thomas' Calculus (14th Edition)
Calculus
ISBN:
9780134438986
Author:
Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:
PEARSON

Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:
9780134763644
Author:
William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:
PEARSON

Calculus: Early Transcendentals
Calculus
ISBN:
9781285741550
Author:
James Stewart
Publisher:
Cengage Learning

Thomas' Calculus (14th Edition)
Calculus
ISBN:
9780134438986
Author:
Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:
PEARSON

Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:
9780134763644
Author:
William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:
PEARSON

Calculus: Early Transcendentals
Calculus
ISBN:
9781319050740
Author:
Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:
W. H. Freeman


Calculus: Early Transcendental Functions
Calculus
ISBN:
9781337552516
Author:
Ron Larson, Bruce H. Edwards
Publisher:
Cengage Learning