For X and Y normed linear spaces, let {Tn} be a sequence in L(X,Y) such that Tn → T in L(X,Y) and let {un} be a sequence in X such that un → u in X. (a) Let e = 1 in the definition of convergence of {Tn} to T in L(X,Y). ||Tn|| < M, Vn e N, where M = sup{||T||, ||T2||, . . , [[TN-1||, 1 + ||T||}, for some N e N. (b) for all n E N, ||Tn(Un) – T(u)||y < ||Tn|| |n – u||x + |Tn – T|| · ||u||x . Use (a) and (b) to show that Tn(Un) → T(u) in Y.
For X and Y normed linear spaces, let {Tn} be a sequence in L(X,Y) such that Tn → T in L(X,Y) and let {un} be a sequence in X such that un → u in X. (a) Let e = 1 in the definition of convergence of {Tn} to T in L(X,Y). ||Tn|| < M, Vn e N, where M = sup{||T||, ||T2||, . . , [[TN-1||, 1 + ||T||}, for some N e N. (b) for all n E N, ||Tn(Un) – T(u)||y < ||Tn|| |n – u||x + |Tn – T|| · ||u||x . Use (a) and (b) to show that Tn(Un) → T(u) in Y.
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question

Transcribed Image Text:For X and Y normed linear spaces, let {Tn} be a sequence in L(X,Y) such that Tn →T in L(X,Y)
and let {un} be a sequence in X such that un → u in X.
(a) Let ɛ = 1 in the definition of convergence of {Tn} to T in L(X,Y).
||Tn|| < M, Vn E N, where M = sup{||T1||, ||T2||,
||TN-1||, 1+ ||T||}, for some N E N.
....,
(b) for all n E N, ||Tn(un) – T(u)||y < ||Tn|| ||Uun – u||x + ||Tn – T|| - ||u||x.
Use (a) and (b) to show that Tn(Um)
→ T(u) in Y.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by step
Solved in 2 steps with 2 images

Follow-up Questions
Read through expert solutions to related follow-up questions below.
Follow-up Question
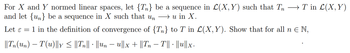
Transcribed Image Text:For X and Y normed linear spaces, let {T} be a sequence in L(X, Y) such that Tn → T in L(X,Y)
and let {n} be a sequence in X such that un → u in X.
Let ε = 1 in the definition of convergence of {T} to T in L(X, Y). Show that for all n ≤ N,
||Tn(Un) – T(u)||y ≤ ||Tn|| · ||Un − U||x + ||Tn − T|| · ||u||x.
Solution
Similar questions
Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

