For what sampling distribution works for?
For what sampling distribution works for?
Concept of sampling distribution:
Let a particular characteristic of a population is of interest in a study. Denote µ as the population mean of that characteristic and σ as the population standard deviation of that characteristic.
Now, it is not always possible to study every population unit. So, a sample of size n is taken from the population.
Let X denotes the random variable that measures the particular characteristic of interest. Let, X1, X2, …, Xn be the values of the random variable for the n units of the sample.
Then, the sample mean has a sampling distribution that has population mean or expected value same as that of X and population standard deviation, called the standard error, which is the population standard deviation of X divided by the square root of the sample size n. The parameters are as follows:
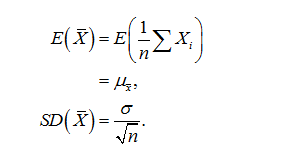
A few points to note:
- The expected value of the sample mean is the population mean. If several samples are taken and their means calculated, then the expectation will be the given population mean. This does not mean that the sample mean for every sample will always be equal to the population mean.
- The sample mean may take only some discrete values or continuous values within a given interval. Depending upon this, the sampling distribution of the sample mean may be either discrete or continuous.
- The expectation and standard deviation for the sampling distribution of the sample mean is as described in the concept. Now, for a large sample size (a sample size of at least 30 is typically considered as “large”), the sampling distribution is approximately normal. Unless the sample size is large enough, the sampling distribution is not normal.
- The standard error of the sample mean is the standard deviation of the sample mean. Note that, in the concept, the standard deviation of the sample mean is (σ ∕√n). Now, the sample size, n is always at least 1. As a result, √n ≥ 1, always. This means that (1∕√n) ≤ 1, always. Hence, (σ ∕√n) ≤ σ, always. Evidently, the standard error of the sample mean will always be smaller than σ.
Step by step
Solved in 3 steps with 1 images









