For the geometric distribution, show that p(x) = 1 and derive the for F(x). 1.14 expression x=1 Hint: Use the geometric series.
For the geometric distribution, show that p(x) = 1 and derive the for F(x). 1.14 expression x=1 Hint: Use the geometric series.
A First Course in Probability (10th Edition)
10th Edition
ISBN:9780134753119
Author:Sheldon Ross
Publisher:Sheldon Ross
Chapter1: Combinatorial Analysis
Section: Chapter Questions
Problem 1.1P: a. How many different 7-place license plates are possible if the first 2 places are for letters and...
Related questions
Question
100%
Please answer question 1.14. Thanks

Transcribed Image Text:Johnsbi bas nsl
1.13 Show that o²= [ (x – µ)² ƒ(x) dx = | x² f(x) dx – µ²
%3D
1.14 For the geometric distribution, show that p(x) = 1 and derive the expression
for F(x).
%3D
x=1
26
ms Hint: Use the geometric series.
1.15 One approach for estimating parameters of a distribution is known as the method of
moments. Consider for example the rectangular distribution where f(x) = 1/(b – a),
a <x< b. By setting the sample mean x (first moment) and sample variance s2 (2nd
moment about the mean) equal to the distribution's mean and variance expressed in
terms of its parameters a and b, the two equations can be solved simultaneously for
their values. Find the method of moments estimators for the rectangular distribution.
%3D
W no
Expert Solution
Step 1
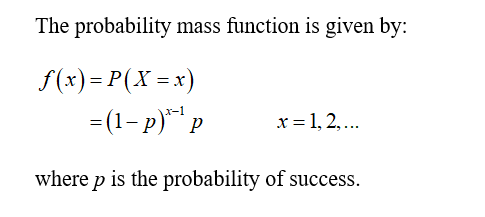
Trending now
This is a popular solution!
Step by step
Solved in 2 steps with 2 images

Recommended textbooks for you

A First Course in Probability (10th Edition)
Probability
ISBN:
9780134753119
Author:
Sheldon Ross
Publisher:
PEARSON


A First Course in Probability (10th Edition)
Probability
ISBN:
9780134753119
Author:
Sheldon Ross
Publisher:
PEARSON
