Radiography & Tomography in Linear Algebra 2015-2018 T. Asaki, H. Moon, M. Snipes 2. Describe the set of all invisible objects. This could involve an equation that the entries would have to satisfy or a few specific objects that could be used to construct all other such objects. Be creative. 3. Describe the set of radiographs that can be produced from all possible objects. This may require similar creativity. Task 3 Now let's tie this back to formal linear algebra definitions. 1. Show that the set of all invisible objects is a subspace of the vector space of all objects. 2. Find a basis for the space of all invisible objects. 3. Find a basis for the set of all possible radiographs.
Radiography & Tomography in Linear Algebra 2015-2018 T. Asaki, H. Moon, M. Snipes 2. Describe the set of all invisible objects. This could involve an equation that the entries would have to satisfy or a few specific objects that could be used to construct all other such objects. Be creative. 3. Describe the set of radiographs that can be produced from all possible objects. This may require similar creativity. Task 3 Now let's tie this back to formal linear algebra definitions. 1. Show that the set of all invisible objects is a subspace of the vector space of all objects. 2. Find a basis for the space of all invisible objects. 3. Find a basis for the set of all possible radiographs.
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question

Transcribed Image Text:Radiography & Tomography in Linear Algebra 2015-2018 T. Asaki, H. Moon, M. Snipes
2. Describe the set of all invisible objects. This could involve an equation that the entries
would have to satisfy or a few specific objects that could be used to construct all other
such objects. Be creative.
3. Describe the set of radiographs that can be produced from all possible objects. This
may require similar creativity.
Task 3
Now let's tie this back to formal linear algebra definitions.
1. Show that the set of all invisible objects is a subspace of the vector space of all objects.
2. Find a basis for the space of all invisible objects.
3. Find a basis for the set of all possible radiographs.

Transcribed Image Text:Radiography and Tomography
Lab 3: Tomography Revisited
In this activity, you will explore some of the properties of radiographic transformations.
In Lab #2 you found several radiographic transformation operators. The object image
consisted of four (or in one case, sixteen) voxels and was represented as a vector in R¹.
The radiographic image was represented as a vector in RM, one entry for each radiographic
pixel. The price we pay for this representation is that we no longer have the geometry of
the radiographic setup encoded in the representation. The use of representations in R" is a
computational tool and not geometrically descriptive of vector spaces of images. We want
to reiterate that this is only a representation and that these images are not vectors in RM.
Because of these new image representations, each transformation could be constructed as a
matrix operator in MMX4(R).
Task 1
For the radiographic transformation 3 which you found in Lab 2 answer the following ques-
tions. Justify your conclusions. For ease, the scenario for transformation 3 is given here.
3.
• Height and width of image in voxels: n = 2 (Total voxels N = 4)
• Pixels per view in radiograph: m = 2
• ScaleFac = √2
Number of views: a = 2
• Angle of the views: 0₁ = 45°, 0₂ = 135°
1. Is it possible for two different objects to produce the same radiograph? If so, give an
example.
2. Are any nonzero objects invisible to this operator? If so, give an example. We say that
an object is nonzero if not all entries are zero. We say that an object is invisible if it
produces the zero radiograph.
3. Are there radiographs (in the appropriate dimension for the problem) that cannot be
produced as the radiograph of any object? If so, give an example.
Task 2
Go a little deeper into understanding the operator by answering these questions.
1. Choose any two objects that produce the same radiograph and subtract them. What
is special about the resulting object?
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution!
Trending now
This is a popular solution!
Step by step
Solved in 4 steps

Follow-up Questions
Read through expert solutions to related follow-up questions below.
Follow-up Question
For Question 3 of task one it states that the transformation matrix for this opertator is invertible. It is not however, this is singular. Does that change Q3 on task 1?
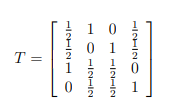
Transcribed Image Text:HIGHINO H
IN IN
HINTIN
HIGHINO
0
T=
Solution
Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

