Homework Help is Here – Start Your Trial Now!
Engineering
Computer Engineering
For each of the functions in the FUNCTION table, determine if they are Big-0 or Big-Omega of the functions listed in the Options table. Also, find Big-Theta of each function (your answer may not be one of the functions in the OPTIONS table). Follow the example shown below. OPTIONS TABLE: √x x³ FUNCTION TABLE: Function Example: f(x)=3x+x³ ƒ(x)= 3x² +log.x¹0 g(x)=2*+xlogx h(x) = log(x³ + 3x² +1) k(x) = 3x²log 2* 3x³ + 2x x² +10 h(x) = log(x!+x*) X 2* Big-0 2³, x³ x² xlogx Big-Omega √x, x, x², xlogx x³, x² logx, log x log.x x² log x Big Theta

For each of the functions in the FUNCTION table, determine if they are Big-0 or Big-Omega of the functions listed in the Options table. Also, find Big-Theta of each function (your answer may not be one of the functions in the OPTIONS table). Follow the example shown below. OPTIONS TABLE: √x x³ FUNCTION TABLE: Function Example: f(x)=3x+x³ ƒ(x)= 3x² +log.x¹0 g(x)=2*+xlogx h(x) = log(x³ + 3x² +1) k(x) = 3x²log 2* 3x³ + 2x x² +10 h(x) = log(x!+x*) X 2* Big-0 2³, x³ x² xlogx Big-Omega √x, x, x², xlogx x³, x² logx, log x log.x x² log x Big Theta

Computer Networking: A Top-Down Approach (7th Edition)
Computer Networking: A Top-Down Approach (7th Edition)
7th Edition
ISBN:9780133594140
Author:James Kurose, Keith Ross
Publisher:James Kurose, Keith Ross
Chapter1: Computer Networks And The Internet
Section: Chapter Questions
Problem R1RQ: What is the difference between a host and an end system? List several different types of end...
See similar textbooks
icon
Related questions
Question
### Analysis of Functions for Big-O, Big-Omega, and Big-Theta Notation #### Instructions For each of the functions in the FUNCTION table below, determine if they are Big-O or Big-Omega of the functions listed in the Options table. Also, find Big-Theta of each function (your answer may not be one of the functions in the OPTIONS table). Follow the example provided. #### Options Table | \(\sqrt{x}\) | \(x\) | \(x^2\) | \(\log x\) | |---|---|---|---| | \(x^3\) | \(2^x\) | \(x \log x\) | \(x^2 \log x\) | #### Function Analysis Table | Function | Big-O | Big-Omega | Big-Theta | |---|---|---|---| | **Example:** \(f(x) = 3x + x^3\) | \(2^x, x^3\) | \(\sqrt{x}, x, x^2, x \log x\)<br> \(x^3, x^2 \log x, \log x\) | \(x^3\) | | \(f(x) = 3x^2 + \log x^{10}\) | | | | | \(g(x) = 2^x + x \log x\) | | | | | \(h(x) = \log (x^3 + 3x^2 + 1)\) | | | | | \(k(x) = 3x^2 \log 2^x\) | | | | | \(f(x) = \frac{3x^5 + 2x}{x^2 + 10}\) | | | | | \(h(x) = \log (x! + x^x)\) | | | | ### Explanation For the given functions, you will identify the growth rates using Big-O, Big-Omega, and Big-Theta notation. - **Big-O notation** describes an upper bound on the growth rate of the function. - **Big-Omega (\(\Omega\)) notation** describes a lower bound on the growth rate of the function. - **Big-Theta (\(\Theta\))
Transcribed Image Text:### Analysis of Functions for Big-O, Big-Omega, and Big-Theta Notation #### Instructions For each of the functions in the FUNCTION table below, determine if they are Big-O or Big-Omega of the functions listed in the Options table. Also, find Big-Theta of each function (your answer may not be one of the functions in the OPTIONS table). Follow the example provided. #### Options Table | \(\sqrt{x}\) | \(x\) | \(x^2\) | \(\log x\) | |---|---|---|---| | \(x^3\) | \(2^x\) | \(x \log x\) | \(x^2 \log x\) | #### Function Analysis Table | Function | Big-O | Big-Omega | Big-Theta | |---|---|---|---| | **Example:** \(f(x) = 3x + x^3\) | \(2^x, x^3\) | \(\sqrt{x}, x, x^2, x \log x\)<br> \(x^3, x^2 \log x, \log x\) | \(x^3\) | | \(f(x) = 3x^2 + \log x^{10}\) | | | | | \(g(x) = 2^x + x \log x\) | | | | | \(h(x) = \log (x^3 + 3x^2 + 1)\) | | | | | \(k(x) = 3x^2 \log 2^x\) | | | | | \(f(x) = \frac{3x^5 + 2x}{x^2 + 10}\) | | | | | \(h(x) = \log (x! + x^x)\) | | | | ### Explanation For the given functions, you will identify the growth rates using Big-O, Big-Omega, and Big-Theta notation. - **Big-O notation** describes an upper bound on the growth rate of the function. - **Big-Omega (\(\Omega\)) notation** describes a lower bound on the growth rate of the function. - **Big-Theta (\(\Theta\))
Expert Solution
trending now

Trending now

This is a popular solution!

steps

Step by step

Solved in 2 steps

SEE SOLUTIONCheck out a sample Q&A here
Blurred answer
Follow-up Questions
Read through expert solutions to related follow-up questions below.
Follow-up Question
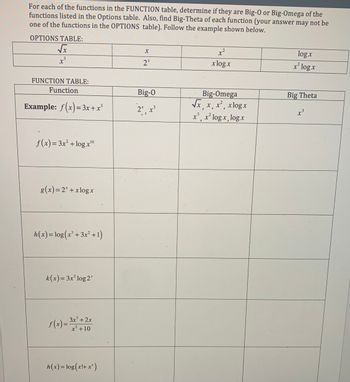
For each of the functions in the FUNCTION table, determine if they are Big-O or Big-Omega of the functions listed in the Options table. Also, find Big-Theta of each function (your answer may not be one of the functions in the OPTIONS table). Follow the example shown below. OPTIONS TABLE: √x x³ FUNCTION TABLE: Function Example: f(x)=3x+x³ f(x)= 3x² +log.x¹0 10 g(x)=2*+xlogx h(x)= log(x³ +3x² +1) k(x) = 3x² log2* f(x) = 3x²+2x x² +10 h(x) = log(x!+x*) X 2x Big-0 2*, x³ x² x log x Big-Omega √x, x, x², xlogx x³, x² logx, log x log x x² log x Big Theta 3 x³
Transcribed Image Text:For each of the functions in the FUNCTION table, determine if they are Big-O or Big-Omega of the functions listed in the Options table. Also, find Big-Theta of each function (your answer may not be one of the functions in the OPTIONS table). Follow the example shown below. OPTIONS TABLE: √x x³ FUNCTION TABLE: Function Example: f(x)=3x+x³ f(x)= 3x² +log.x¹0 10 g(x)=2*+xlogx h(x)= log(x³ +3x² +1) k(x) = 3x² log2* f(x) = 3x²+2x x² +10 h(x) = log(x!+x*) X 2x Big-0 2*, x³ x² x log x Big-Omega √x, x, x², xlogx x³, x² logx, log x log x x² log x Big Theta 3 x³
Solution
Bartleby Expert
SEE SOLUTION
Recommended textbooks for you
Computer Networking: A Top-Down Approach (7th Edi…
Computer Networking: A Top-Down Approach (7th Edi…
Computer Engineering
ISBN:
9780133594140
Author:
James Kurose, Keith Ross
Publisher:
PEARSON
Computer Organization and Design MIPS Edition, Fi…
Computer Organization and Design MIPS Edition, Fi…
Computer Engineering
ISBN:
9780124077263
Author:
David A. Patterson, John L. Hennessy
Publisher:
Elsevier Science
Network+ Guide to Networks (MindTap Course List)
Network+ Guide to Networks (MindTap Course List)
Computer Engineering
ISBN:
9781337569330
Author:
Jill West, Tamara Dean, Jean Andrews
Publisher:
Cengage Learning
Concepts of Database Management
Concepts of Database Management
Computer Engineering
ISBN:
9781337093422
Author:
Joy L. Starks, Philip J. Pratt, Mary Z. Last
Publisher:
Cengage Learning
Prelude to Programming
Prelude to Programming
Computer Engineering
ISBN:
9780133750423
Author:
VENIT, Stewart
Publisher:
Pearson Education
Sc Business Data Communications and Networking, T…
Sc Business Data Communications and Networking, T…
Computer Engineering
ISBN:
9781119368830
Author:
FITZGERALD
Publisher:
WILEY
SEE MORE TEXTBOOKS