Calculus: Early Transcendentals
8th Edition
ISBN:9781285741550
Author:James Stewart
Publisher:James Stewart
Chapter1: Functions And Models
Section: Chapter Questions
Problem 1RCC: (a) What is a function? What are its domain and range? (b) What is the graph of a function? (c) How...
Related questions
Question
I need help finding the 2nd derivative of y. I believe I'm on the right track but I'm not sure how to continue.
![**Objective:** Find the first and second derivatives, \( y' \) and \( y'' \).
**Given Function:**
\[ y = \sqrt{\sin(x)} \]
**First Derivative (\( y' \)):**
The derivative is calculated as:
\[ y' = \frac{\cos(x)}{2\sqrt{\sin(x)}} \]
**Second Derivative (\( y'' \)):**
The second derivative is not provided and is expected to be calculated based on \( y' \).
**Explanation:**
To find the first derivative of \( y = \sqrt{\sin(x)} \), you can use the chain rule. The process involves differentiating the outer and inner functions.
1. The outer function is \( u^{1/2} \), where \( u = \sin(x) \), giving the derivative as \( \frac{1}{2}u^{-1/2} \).
2. The inner function is \( u = \sin(x) \), whose derivative is \( \cos(x) \).
Thus, combining these using the chain rule results in:
\[ y' = \frac{1}{2} (\sin(x))^{-1/2} \cdot \cos(x) = \frac{\cos(x)}{2\sqrt{\sin(x)}} \]
The second derivative \( y'' \) requires further differentiation of \( y' \).](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F3eb03a80-7cae-4d33-b228-e2e0361c370e%2Fffae9de3-591e-4f79-9f70-87014a586ceb%2Fhpft2zq_processed.png&w=3840&q=75)
Transcribed Image Text:**Objective:** Find the first and second derivatives, \( y' \) and \( y'' \).
**Given Function:**
\[ y = \sqrt{\sin(x)} \]
**First Derivative (\( y' \)):**
The derivative is calculated as:
\[ y' = \frac{\cos(x)}{2\sqrt{\sin(x)}} \]
**Second Derivative (\( y'' \)):**
The second derivative is not provided and is expected to be calculated based on \( y' \).
**Explanation:**
To find the first derivative of \( y = \sqrt{\sin(x)} \), you can use the chain rule. The process involves differentiating the outer and inner functions.
1. The outer function is \( u^{1/2} \), where \( u = \sin(x) \), giving the derivative as \( \frac{1}{2}u^{-1/2} \).
2. The inner function is \( u = \sin(x) \), whose derivative is \( \cos(x) \).
Thus, combining these using the chain rule results in:
\[ y' = \frac{1}{2} (\sin(x))^{-1/2} \cdot \cos(x) = \frac{\cos(x)}{2\sqrt{\sin(x)}} \]
The second derivative \( y'' \) requires further differentiation of \( y' \).
![This image contains the step-by-step differentiation of a mathematical function using the quotient rule. Below is a detailed transcription suitable for an educational website:
---
**Quotient Rule Differentiation**
Given:
\[ y' = \frac{\cos(x)}{2\sqrt{\sin(x)}} \]
To differentiate using the quotient rule, we follow these steps:
1. **Identify the Functions:**
- Let \( f(x) = \cos(x) \) and \( g(x) = 2\sqrt{\sin(x)} \).
- The derivative using the quotient rule is \(\frac{gf' - fg'}{g^2}\).
2. **Apply the Quotient Rule:**
\[
y'' = \frac{2\sqrt{\sin(x)} \cdot \frac{d}{dx}[\cos(x)] - \cos(x) \cdot \frac{d}{dx}[2\sqrt{\sin(x)}]}{(2\sqrt{\sin(x)})^2}
\]
3. **Calculate the Derivatives:**
- Derivative of \(\cos(x)\) is \( -\sin(x) \).
- Differentiate \(2\sqrt{\sin(x)}\) using the chain rule:
\[
2 \cdot \frac{d}{dx}\left[ \sin(x)^{1/2} \right] = 2 \cdot \frac{1}{2} \cdot \sin(x)^{-1/2} \cdot \frac{d}{dx}[\sin(x)]
\]
4. **Substitute and Simplify:**
\[
y'' = \frac{2\sqrt{\sin(x)} \cdot (-\sin(x)) - \cos(x) \cdot 2 \cdot \left(\frac{1}{2} \cdot \sin(x)^{-1/2} \cdot \cos(x)\right)}{(2\sqrt{\sin(x)})^2}
\]
5. **Final Simplified Expression:**
\[
y'' = \frac{2\sqrt{\sin(x)} \cdot (-\sin(x)) - \cos(x) \cdot \sin(x)^{-1/2} \cdot \cos(x)}{(2\sqrt{\sin(x)})^2}](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F3eb03a80-7cae-4d33-b228-e2e0361c370e%2Fffae9de3-591e-4f79-9f70-87014a586ceb%2Fw0hxfs_processed.png&w=3840&q=75)
Transcribed Image Text:This image contains the step-by-step differentiation of a mathematical function using the quotient rule. Below is a detailed transcription suitable for an educational website:
---
**Quotient Rule Differentiation**
Given:
\[ y' = \frac{\cos(x)}{2\sqrt{\sin(x)}} \]
To differentiate using the quotient rule, we follow these steps:
1. **Identify the Functions:**
- Let \( f(x) = \cos(x) \) and \( g(x) = 2\sqrt{\sin(x)} \).
- The derivative using the quotient rule is \(\frac{gf' - fg'}{g^2}\).
2. **Apply the Quotient Rule:**
\[
y'' = \frac{2\sqrt{\sin(x)} \cdot \frac{d}{dx}[\cos(x)] - \cos(x) \cdot \frac{d}{dx}[2\sqrt{\sin(x)}]}{(2\sqrt{\sin(x)})^2}
\]
3. **Calculate the Derivatives:**
- Derivative of \(\cos(x)\) is \( -\sin(x) \).
- Differentiate \(2\sqrt{\sin(x)}\) using the chain rule:
\[
2 \cdot \frac{d}{dx}\left[ \sin(x)^{1/2} \right] = 2 \cdot \frac{1}{2} \cdot \sin(x)^{-1/2} \cdot \frac{d}{dx}[\sin(x)]
\]
4. **Substitute and Simplify:**
\[
y'' = \frac{2\sqrt{\sin(x)} \cdot (-\sin(x)) - \cos(x) \cdot 2 \cdot \left(\frac{1}{2} \cdot \sin(x)^{-1/2} \cdot \cos(x)\right)}{(2\sqrt{\sin(x)})^2}
\]
5. **Final Simplified Expression:**
\[
y'' = \frac{2\sqrt{\sin(x)} \cdot (-\sin(x)) - \cos(x) \cdot \sin(x)^{-1/2} \cdot \cos(x)}{(2\sqrt{\sin(x)})^2}
Expert Solution
Step 1: The given information is
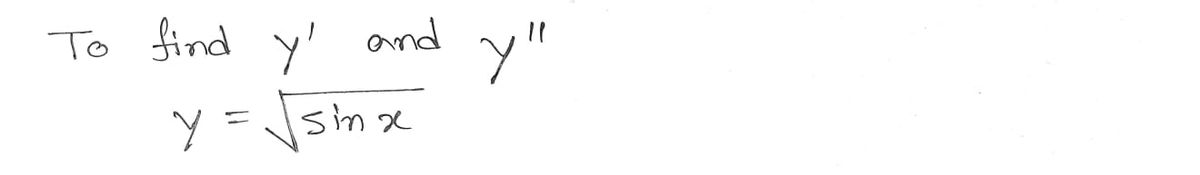
Trending now
This is a popular solution!
Step by step
Solved in 3 steps with 3 images

Follow-up Questions
Read through expert solutions to related follow-up questions below.
Follow-up Question
Could you explain the last two parts to me? How do you go from sin(x)3/2 to sin2(x)?
And where did square root of sin(x) go? Did you somehow move it to the denominator?
Solution
Recommended textbooks for you

Calculus: Early Transcendentals
Calculus
ISBN:
9781285741550
Author:
James Stewart
Publisher:
Cengage Learning

Thomas' Calculus (14th Edition)
Calculus
ISBN:
9780134438986
Author:
Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:
PEARSON

Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:
9780134763644
Author:
William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:
PEARSON

Calculus: Early Transcendentals
Calculus
ISBN:
9781285741550
Author:
James Stewart
Publisher:
Cengage Learning

Thomas' Calculus (14th Edition)
Calculus
ISBN:
9780134438986
Author:
Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:
PEARSON

Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:
9780134763644
Author:
William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:
PEARSON

Calculus: Early Transcendentals
Calculus
ISBN:
9781319050740
Author:
Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:
W. H. Freeman


Calculus: Early Transcendental Functions
Calculus
ISBN:
9781337552516
Author:
Ron Larson, Bruce H. Edwards
Publisher:
Cengage Learning