Find the volume of the solid generated by rotating the infinite region in the first quadrant between y = ex and the x-axis about the x-axis. The volume is (Simplify your answer. Type an exact answer, using as needed.)
Find the volume of the solid generated by rotating the infinite region in the first quadrant between y = ex and the x-axis about the x-axis. The volume is (Simplify your answer. Type an exact answer, using as needed.)
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
![**Problem Statement:**
Find the volume of the solid generated by rotating the infinite region in the first quadrant between \( y = e^{-x} \) and the x-axis about the x-axis.
---
**Solution Approach:**
To solve this problem, you will typically use the method of disks or washers for finding the volume of a solid of revolution.
**Step-by-step Explanation:**
1. **Identify the function and axis of rotation:**
- Function: \( y = e^{-x} \)
- Axis of rotation: x-axis
2. **Determine the intersection points:**
- The region of interest is infinite along the x-axis as \( y = e^{-x} \) approaches zero.
3. **Set up the integral using the disk method:**
- The radius of each disk is given by the function value at a particular x, which is \( e^{-x} \).
- The volume \( V \) of the solid generated is given by the integral:
\[
V = \pi \int_{0}^{\infty} (e^{-x})^2 \, dx
\]
4. **Simplify and solve the integral:**
- Simplify the integrand: \( (e^{-x})^2 = e^{-2x} \)
- The volume integral becomes:
\[
V = \pi \int_{0}^{\infty} e^{-2x} \, dx
\]
5. **Evaluate the integral:**
- The integral of \( e^{-2x} \) is \( -\frac{1}{2} e^{-2x} \).
- Evaluate from 0 to \( \infty \):
\[
V = \pi \left[ -\frac{1}{2} e^{-2x} \right]_{0}^{\infty} = \pi \left( 0 + \frac{1}{2} \right) = \frac{\pi}{2}
\]
**Final Answer:**
The volume is \( \frac{\pi}{2} \).
(Simplify your answer. Type an exact answer, using \(\pi\) as needed.)](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F6851e105-8727-4477-9935-da490bfe86c3%2F8e5d6aca-7b8d-4627-a807-67e4e7d59694%2Fux0j7tc_processed.jpeg&w=3840&q=75)
Transcribed Image Text:**Problem Statement:**
Find the volume of the solid generated by rotating the infinite region in the first quadrant between \( y = e^{-x} \) and the x-axis about the x-axis.
---
**Solution Approach:**
To solve this problem, you will typically use the method of disks or washers for finding the volume of a solid of revolution.
**Step-by-step Explanation:**
1. **Identify the function and axis of rotation:**
- Function: \( y = e^{-x} \)
- Axis of rotation: x-axis
2. **Determine the intersection points:**
- The region of interest is infinite along the x-axis as \( y = e^{-x} \) approaches zero.
3. **Set up the integral using the disk method:**
- The radius of each disk is given by the function value at a particular x, which is \( e^{-x} \).
- The volume \( V \) of the solid generated is given by the integral:
\[
V = \pi \int_{0}^{\infty} (e^{-x})^2 \, dx
\]
4. **Simplify and solve the integral:**
- Simplify the integrand: \( (e^{-x})^2 = e^{-2x} \)
- The volume integral becomes:
\[
V = \pi \int_{0}^{\infty} e^{-2x} \, dx
\]
5. **Evaluate the integral:**
- The integral of \( e^{-2x} \) is \( -\frac{1}{2} e^{-2x} \).
- Evaluate from 0 to \( \infty \):
\[
V = \pi \left[ -\frac{1}{2} e^{-2x} \right]_{0}^{\infty} = \pi \left( 0 + \frac{1}{2} \right) = \frac{\pi}{2}
\]
**Final Answer:**
The volume is \( \frac{\pi}{2} \).
(Simplify your answer. Type an exact answer, using \(\pi\) as needed.)
Expert Solution
Step 1: Given information
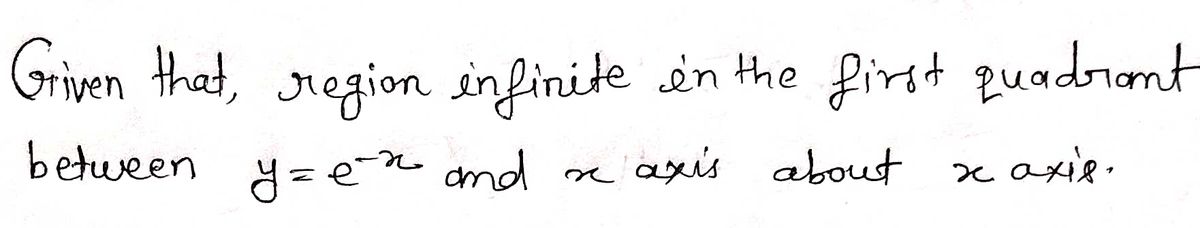
Step by step
Solved in 3 steps with 2 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

