Find the volume of the solid formed by rotating the region enclosed by у 3 е + 5, у — 0, х — 0, х — 0.1 about the x-axis.
Find the volume of the solid formed by rotating the region enclosed by у 3 е + 5, у — 0, х — 0, х — 0.1 about the x-axis.
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
![**Problem Statement:**
Find the volume of the solid formed by rotating the region enclosed by the curves and lines:
- \( y = e^{2x} + 5 \)
- \( y = 0 \)
- \( x = 0 \)
- \( x = 0.1 \)
about the x-axis.
**Explanation:**
To solve this problem, we need to compute the volume of a solid of revolution. This is typically achieved using the disk or washer method, depending on the nature of the region.
1. **Function:** \( y = e^{2x} + 5 \)
- This is an exponential function shifted upward by 5 units. It describes the upper boundary of the region.
2. **Boundaries:**
- \( y = 0 \) represents the x-axis, serving as the lower boundary.
- \( x = 0 \) and \( x = 0.1 \) are vertical lines, defining the left and right boundaries, respectively.
3. **Rotation About the x-axis:**
- When rotating around the x-axis, the area between the curve \( y = e^{2x} + 5 \) and the line \( y = 0 \) is revolved to create a 3-dimensional solid.
**Visual Details:**
- **No Graph/Diagram Provided:** Since no graph or diagram is present in the image, the task is focused on describing the process rather than illustrating it visually.
- **Understanding the Area of Revolution:** You can imagine the shaded region between the curve and the x-axis being rotated around the x-axis to form a solid resembling a stack of infinitesimally thin disks.
To find the volume of the solid, an integral setup follows:
\[ V = \pi \int_{0}^{0.1} \left(e^{2x} + 5\right)^2 \, dx \]
where \( V \) is the volume, and the integral calculates the sum of the areas of the disks formed by rotating the curve around the x-axis.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F6e916346-eb1f-468f-a417-f3db3524f0d2%2F2f667d0d-79f5-4b28-b014-1fd3e5fa37f7%2F0h8h1zn_processed.png&w=3840&q=75)
Transcribed Image Text:**Problem Statement:**
Find the volume of the solid formed by rotating the region enclosed by the curves and lines:
- \( y = e^{2x} + 5 \)
- \( y = 0 \)
- \( x = 0 \)
- \( x = 0.1 \)
about the x-axis.
**Explanation:**
To solve this problem, we need to compute the volume of a solid of revolution. This is typically achieved using the disk or washer method, depending on the nature of the region.
1. **Function:** \( y = e^{2x} + 5 \)
- This is an exponential function shifted upward by 5 units. It describes the upper boundary of the region.
2. **Boundaries:**
- \( y = 0 \) represents the x-axis, serving as the lower boundary.
- \( x = 0 \) and \( x = 0.1 \) are vertical lines, defining the left and right boundaries, respectively.
3. **Rotation About the x-axis:**
- When rotating around the x-axis, the area between the curve \( y = e^{2x} + 5 \) and the line \( y = 0 \) is revolved to create a 3-dimensional solid.
**Visual Details:**
- **No Graph/Diagram Provided:** Since no graph or diagram is present in the image, the task is focused on describing the process rather than illustrating it visually.
- **Understanding the Area of Revolution:** You can imagine the shaded region between the curve and the x-axis being rotated around the x-axis to form a solid resembling a stack of infinitesimally thin disks.
To find the volume of the solid, an integral setup follows:
\[ V = \pi \int_{0}^{0.1} \left(e^{2x} + 5\right)^2 \, dx \]
where \( V \) is the volume, and the integral calculates the sum of the areas of the disks formed by rotating the curve around the x-axis.
Expert Solution
Step 1
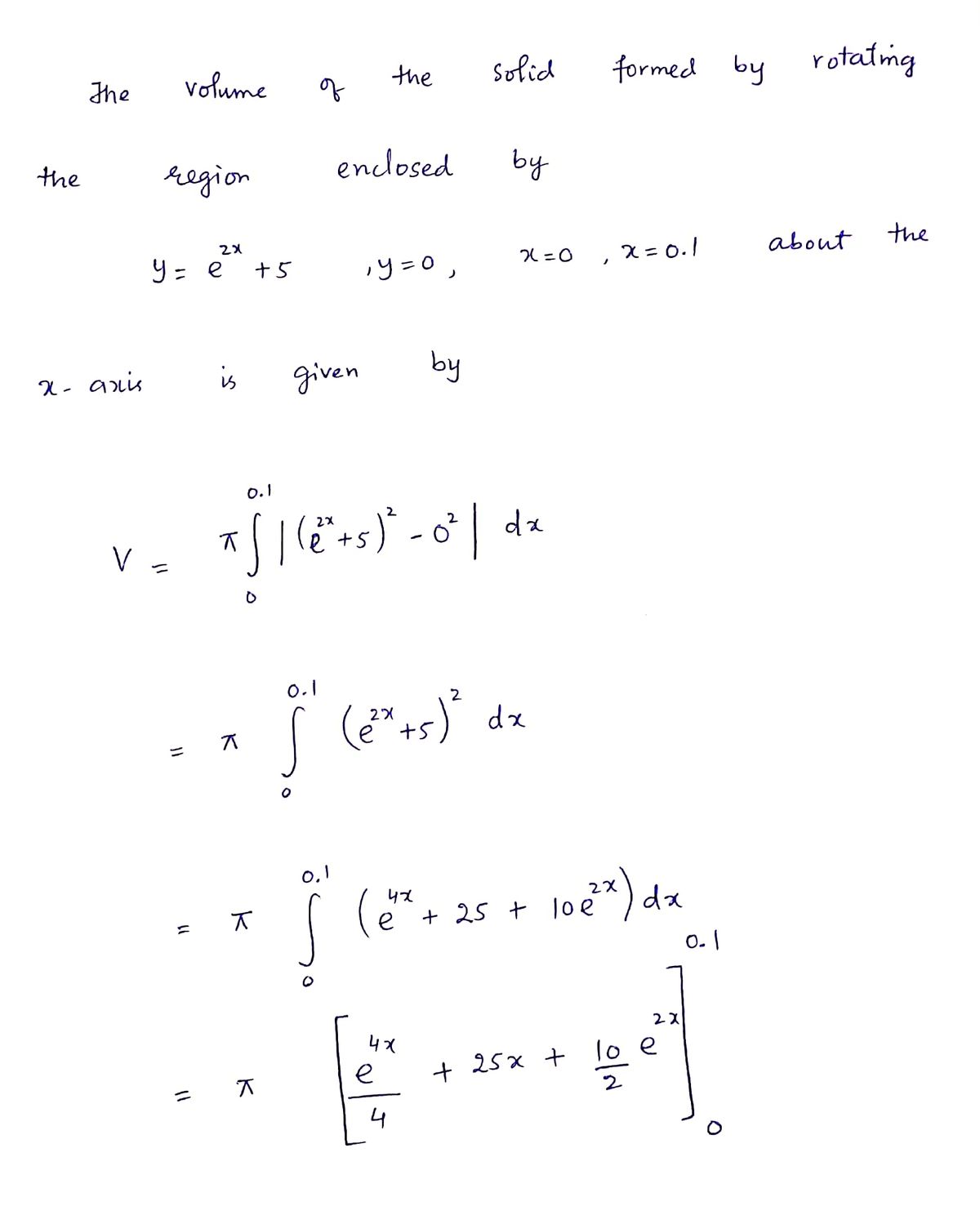
Step by step
Solved in 2 steps with 2 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

