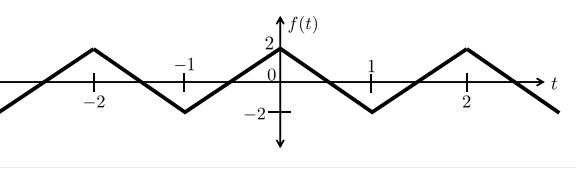
Find the trigonometric Fourier series coefficients of the following signal: -2 -2- ↑f(t) 2
Find the trigonometric Fourier series coefficients of the following signal: -2 -2- ↑f(t) 2
Introductory Circuit Analysis (13th Edition)
13th Edition
ISBN:9780133923605
Author:Robert L. Boylestad
Publisher:Robert L. Boylestad
Chapter1: Introduction
Section: Chapter Questions
Problem 1P: Visit your local library (at school or home) and describe the extent to which it provides literature...
Related questions
Question
Please help answering this question and simplify the answer as much as possible. Please write clearly .

Transcribed Image Text:**Transcription for Educational Website:**
The task is to find the trigonometric Fourier series coefficients of the following signal.
**Graph Explanation:**
- **Axes:** The horizontal axis is labeled \( t \) (time), and the vertical axis is labeled \( f(t) \) (signal amplitude).
- **Signal Description:** The function \( f(t) \) appears to have a triangular waveform.
- **Waveform Pattern:**
- Peaks at \( f(t) = 2 \) and troughs at \( f(t) = -2 \).
- The pattern shows symmetry about the vertical axis, implying it's an even function.
- The waveform repeats every 4 units along the \( t \)-axis, indicating a period of 4.
- **Key Points:**
- The waveform passes through the origin (0,0).
- Linear segments connect points at \( (-2, 0) \) to \( (0, 2) \), \( (0, 2) \) to \( (2, 0) \), and so on, continuing periodically.
This periodic waveform can be analyzed to determine its Fourier series, which will reveal its frequency components.
Expert Solution
Step 1
Calculation of trigonometric Fourier series coefficients of the following signal :
Trending now
This is a popular solution!
Step by step
Solved in 5 steps with 4 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, electrical-engineering and related others by exploring similar questions and additional content below.Recommended textbooks for you

Introductory Circuit Analysis (13th Edition)
Electrical Engineering
ISBN:
9780133923605
Author:
Robert L. Boylestad
Publisher:
PEARSON

Delmar's Standard Textbook Of Electricity
Electrical Engineering
ISBN:
9781337900348
Author:
Stephen L. Herman
Publisher:
Cengage Learning

Programmable Logic Controllers
Electrical Engineering
ISBN:
9780073373843
Author:
Frank D. Petruzella
Publisher:
McGraw-Hill Education

Introductory Circuit Analysis (13th Edition)
Electrical Engineering
ISBN:
9780133923605
Author:
Robert L. Boylestad
Publisher:
PEARSON

Delmar's Standard Textbook Of Electricity
Electrical Engineering
ISBN:
9781337900348
Author:
Stephen L. Herman
Publisher:
Cengage Learning

Programmable Logic Controllers
Electrical Engineering
ISBN:
9780073373843
Author:
Frank D. Petruzella
Publisher:
McGraw-Hill Education

Fundamentals of Electric Circuits
Electrical Engineering
ISBN:
9780078028229
Author:
Charles K Alexander, Matthew Sadiku
Publisher:
McGraw-Hill Education

Electric Circuits. (11th Edition)
Electrical Engineering
ISBN:
9780134746968
Author:
James W. Nilsson, Susan Riedel
Publisher:
PEARSON

Engineering Electromagnetics
Electrical Engineering
ISBN:
9780078028151
Author:
Hayt, William H. (william Hart), Jr, BUCK, John A.
Publisher:
Mcgraw-hill Education,