Find the probability of detecting a photon if the probability amplitude is as provided in the first image. (Hint: See the second attatched image for more on finding the probability amplitude)
Find the probability of detecting a photon if the probability amplitude is as provided in the first image. (Hint: See the second attatched image for more on finding the probability amplitude)
A First Course in Probability (10th Edition)
10th Edition
ISBN:9780134753119
Author:Sheldon Ross
Publisher:Sheldon Ross
Chapter1: Combinatorial Analysis
Section: Chapter Questions
Problem 1.1P: a. How many different 7-place license plates are possible if the first 2 places are for letters and...
Related questions
Question
Find the
(Hint: See the second attatched image for more on finding the probability amplitude)
![The image displays the mathematical expression:
\[
\frac{1}{1+i} + i
\]
Here, \( i \) represents the imaginary unit, which satisfies \( i^2 = -1 \). This expression is a combination of a complex fraction and an imaginary number. It involves dividing 1 by the sum of 1 and the imaginary unit \( i \), and then adding \( i \) to the result. Understanding such expressions is crucial in complex number arithmetic, often used in fields like engineering and physics.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F2aad56e8-dec1-4fb1-9f36-d4803717353d%2F1aa4c5dc-987e-48d0-94a4-911d1b8122c4%2Furu7l5c_processed.png&w=3840&q=75)
Transcribed Image Text:The image displays the mathematical expression:
\[
\frac{1}{1+i} + i
\]
Here, \( i \) represents the imaginary unit, which satisfies \( i^2 = -1 \). This expression is a combination of a complex fraction and an imaginary number. It involves dividing 1 by the sum of 1 and the imaginary unit \( i \), and then adding \( i \) to the result. Understanding such expressions is crucial in complex number arithmetic, often used in fields like engineering and physics.
![1. The probability of detecting a particle is equal to \( z^*z \), where \( z \) is called the probability amplitude and \( z^* \) is its complex conjugate.
2. To determine the probability amplitude for a process that can be viewed as taking place in a series of steps, such as propagation of a photon from a light source to a beam splitter, transmission at the beam splitter, and propagation to a photodetector, we multiply the probability amplitudes for each of these steps:
\[
z = z_a z_b \ldots
\]
3. When there are multiple paths that a particle can take between the source and the detector, the probability amplitude for detecting the particle is the sum of the individual probability amplitudes for the particle to take each path:
\[
z = z_1 + z_2 + \ldots
\]](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F2aad56e8-dec1-4fb1-9f36-d4803717353d%2F1aa4c5dc-987e-48d0-94a4-911d1b8122c4%2Fl9mmm9_processed.png&w=3840&q=75)
Transcribed Image Text:1. The probability of detecting a particle is equal to \( z^*z \), where \( z \) is called the probability amplitude and \( z^* \) is its complex conjugate.
2. To determine the probability amplitude for a process that can be viewed as taking place in a series of steps, such as propagation of a photon from a light source to a beam splitter, transmission at the beam splitter, and propagation to a photodetector, we multiply the probability amplitudes for each of these steps:
\[
z = z_a z_b \ldots
\]
3. When there are multiple paths that a particle can take between the source and the detector, the probability amplitude for detecting the particle is the sum of the individual probability amplitudes for the particle to take each path:
\[
z = z_1 + z_2 + \ldots
\]
Expert Solution
Step 1
Please find the explanation below. Thank you. 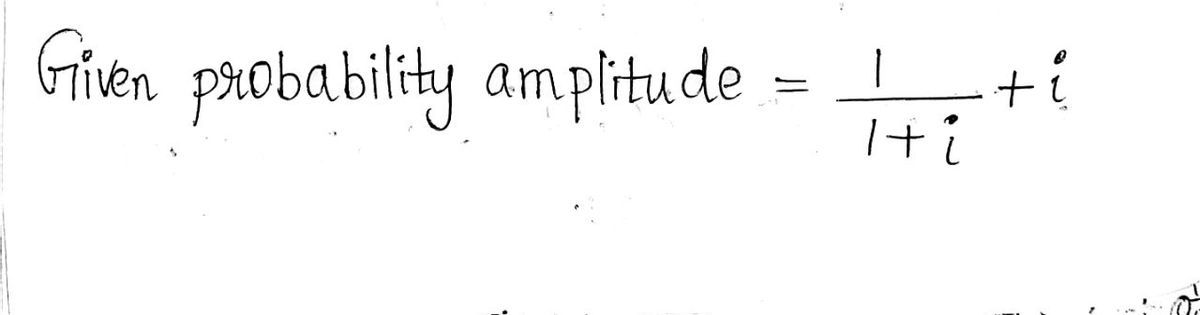
Step by step
Solved in 3 steps with 3 images

Recommended textbooks for you

A First Course in Probability (10th Edition)
Probability
ISBN:
9780134753119
Author:
Sheldon Ross
Publisher:
PEARSON


A First Course in Probability (10th Edition)
Probability
ISBN:
9780134753119
Author:
Sheldon Ross
Publisher:
PEARSON
