Find the objective function in the given problem (in terms of w) if the constraint is that the sum of length and width and height cannot exceed 108 in. Airline regulations Suppose an airline policy states that all baggagemust be box-shaped with a sum of length, width, and height not exceeding 64 in. What are the dimensions and volume of a square-based box with the greatest volume under these conditions?
Find the objective function in the given problem (in terms of w) if the constraint is that the sum of length and width and height cannot exceed 108 in.
Airline regulations Suppose an airline policy states that all baggage
must be box-shaped with a sum of length, width, and height not exceeding 64 in. What are the dimensions and volume of a square-based box with the greatest volume under these conditions?
Note:
Please provide complete instructions for first problem.
Given
The box has a sum of length, width, and height not exceeding 64 in.
Let
length of box = l
width of box = w
height of box = h
Base of box is square
Hence, l=w
And
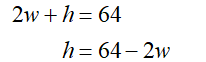
So, volume of square-based box is
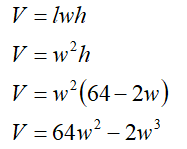
To find dimensions of box for maximum volume ,
Let's find critical points by equating
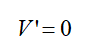
Hence,
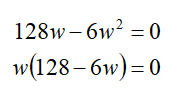
So,

Therefore,
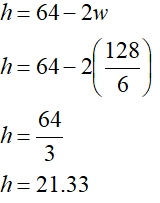
And
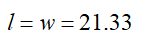
Volume of box is
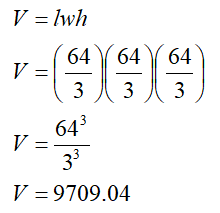
Step by step
Solved in 3 steps with 10 images









