Find the matrix A' = [LA]. Also find an invertible matrix Q such that A' = Q-¹AQ. (a) Suppose W₁ and W₂ are subspaces in a vector space V and that V = W₁ + W₂. Prove that V = W₁ W₂ if and only if any vector v € V can be represented uniquely as v = v₁ + v2 where V₁ € W₁, v₂ € W₂. (b) Suppose W₁ and W₂ are subspaces in a vector space V, and such that V =W₁ W₂. If B₁ is a basis of W₁ and 32 is a basis of W2 prove that 31 U 32 is a basis of V.
Find the matrix A' = [LA]. Also find an invertible matrix Q such that A' = Q-¹AQ. (a) Suppose W₁ and W₂ are subspaces in a vector space V and that V = W₁ + W₂. Prove that V = W₁ W₂ if and only if any vector v € V can be represented uniquely as v = v₁ + v2 where V₁ € W₁, v₂ € W₂. (b) Suppose W₁ and W₂ are subspaces in a vector space V, and such that V =W₁ W₂. If B₁ is a basis of W₁ and 32 is a basis of W2 prove that 31 U 32 is a basis of V.
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
![**Transcription for Educational Website**
---
**Find the matrix \( A' = [L_A]_\beta^\beta \). Also find an invertible matrix \( Q \) such that \( A' = Q^{-1}AQ \).**
(a) Suppose \( W_1 \) and \( W_2 \) are subspaces in a vector space \( V \) and that \( V = W_1 + W_2 \). Prove that \( V = W_1 \oplus W_2 \) if and only if any vector \( v \in V \) can be represented uniquely as \( v = v_1 + v_2 \) where \( v_1 \in W_1, v_2 \in W_2 \).
(b) Suppose \( W_1 \) and \( W_2 \) are subspaces in a vector space \( V \), and such that \( V = W_1 \oplus W_2 \). If \( \beta_1 \) is a basis of \( W_1 \) and \( \beta_2 \) is a basis of \( W_2 \), prove that \( \beta_1 \cup \beta_2 \) is a basis of \( V \).
---](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F32f77ee0-291c-46d0-b315-80fb2fd096d8%2F66e32d85-0ab7-4013-8365-9da3866e8cc7%2Fsqkrpks_processed.jpeg&w=3840&q=75)
Transcribed Image Text:**Transcription for Educational Website**
---
**Find the matrix \( A' = [L_A]_\beta^\beta \). Also find an invertible matrix \( Q \) such that \( A' = Q^{-1}AQ \).**
(a) Suppose \( W_1 \) and \( W_2 \) are subspaces in a vector space \( V \) and that \( V = W_1 + W_2 \). Prove that \( V = W_1 \oplus W_2 \) if and only if any vector \( v \in V \) can be represented uniquely as \( v = v_1 + v_2 \) where \( v_1 \in W_1, v_2 \in W_2 \).
(b) Suppose \( W_1 \) and \( W_2 \) are subspaces in a vector space \( V \), and such that \( V = W_1 \oplus W_2 \). If \( \beta_1 \) is a basis of \( W_1 \) and \( \beta_2 \) is a basis of \( W_2 \), prove that \( \beta_1 \cup \beta_2 \) is a basis of \( V \).
---
Expert Solution
Step 1p
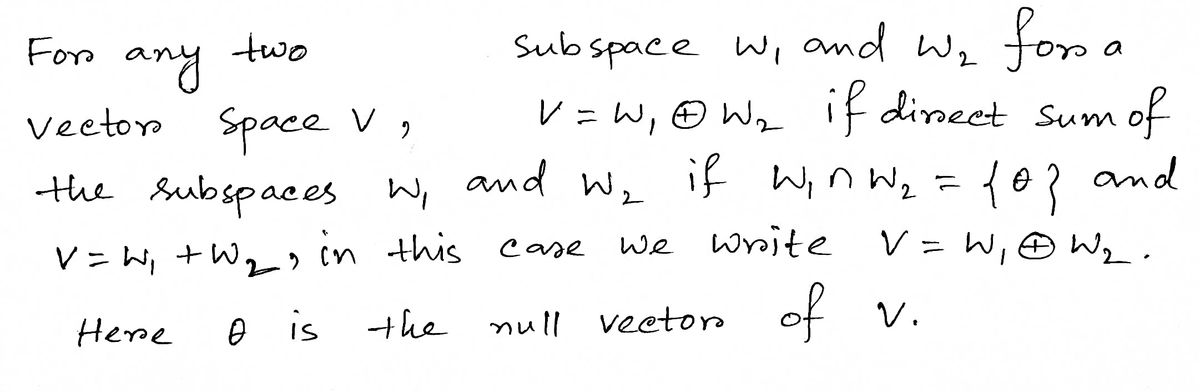
Step by step
Solved in 4 steps with 4 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

