Find the limit, if it exists, or type N if it does not exist. 4x²+5y² lim (x,y) →(-2,4) ev = 2980.9
Find the limit, if it exists, or type N if it does not exist. 4x²+5y² lim (x,y) →(-2,4) ev = 2980.9
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
Please help with homework example
![### Problem Statement
Find the limit, if it exists, or type N if it does not exist.
\[
\lim_{(x,y) \to (-2,4)} e^{\sqrt{4x^2 + 5y^2}} =
\]
**Answer Box:** 2980.9
### Explanation
You are given a multivariable limit problem involving an exponential function with a square root in the exponent. The function is:
\[ e^{\sqrt{4x^2 + 5y^2}} \]
The task is to find the limit as \((x, y)\) approaches \((-2, 4)\).
### Process
1. **Examine the Expression:**
- The function inside the exponent is \(\sqrt{4x^2 + 5y^2}\), which can be seen as an ellipsoidal form.
2. **Approach the Limit:**
- Substitute \(x = -2\) and \(y = 4\) directly into the expression.
- Calculate the expression \(\sqrt{4(-2)^2 + 5(4)^2}\).
3. **Substitution Calculation:**
- \((-2)^2 = 4\), so \(4(-2)^2 = 16\).
- \(4^2 = 16\), so \(5(4)^2 = 80\).
- Add these results to form the expression under the square root: \(16 + 80 = 96\).
4. **Final Calculation:**
- Evaluate \(\sqrt{96}\) and then compute \(e^{\sqrt{96}}\).
5. **Check the Result:**
- The expression should evaluate to approximately 2980.9 as given in the answer box, confirming that the limit exists.
### Conclusion
This problem demonstrates finding a limit involving exponential and radical functions with two variables approaching constant values. The result shows the application of substitution and simplification in multivariable calculus.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F39ee3059-6733-456c-bbc4-46bedd3c18f2%2F4bc4b955-1b43-461f-9d14-7a9194adb7be%2Fvtlpj4_processed.png&w=3840&q=75)
Transcribed Image Text:### Problem Statement
Find the limit, if it exists, or type N if it does not exist.
\[
\lim_{(x,y) \to (-2,4)} e^{\sqrt{4x^2 + 5y^2}} =
\]
**Answer Box:** 2980.9
### Explanation
You are given a multivariable limit problem involving an exponential function with a square root in the exponent. The function is:
\[ e^{\sqrt{4x^2 + 5y^2}} \]
The task is to find the limit as \((x, y)\) approaches \((-2, 4)\).
### Process
1. **Examine the Expression:**
- The function inside the exponent is \(\sqrt{4x^2 + 5y^2}\), which can be seen as an ellipsoidal form.
2. **Approach the Limit:**
- Substitute \(x = -2\) and \(y = 4\) directly into the expression.
- Calculate the expression \(\sqrt{4(-2)^2 + 5(4)^2}\).
3. **Substitution Calculation:**
- \((-2)^2 = 4\), so \(4(-2)^2 = 16\).
- \(4^2 = 16\), so \(5(4)^2 = 80\).
- Add these results to form the expression under the square root: \(16 + 80 = 96\).
4. **Final Calculation:**
- Evaluate \(\sqrt{96}\) and then compute \(e^{\sqrt{96}}\).
5. **Check the Result:**
- The expression should evaluate to approximately 2980.9 as given in the answer box, confirming that the limit exists.
### Conclusion
This problem demonstrates finding a limit involving exponential and radical functions with two variables approaching constant values. The result shows the application of substitution and simplification in multivariable calculus.
Expert Solution
Step 1
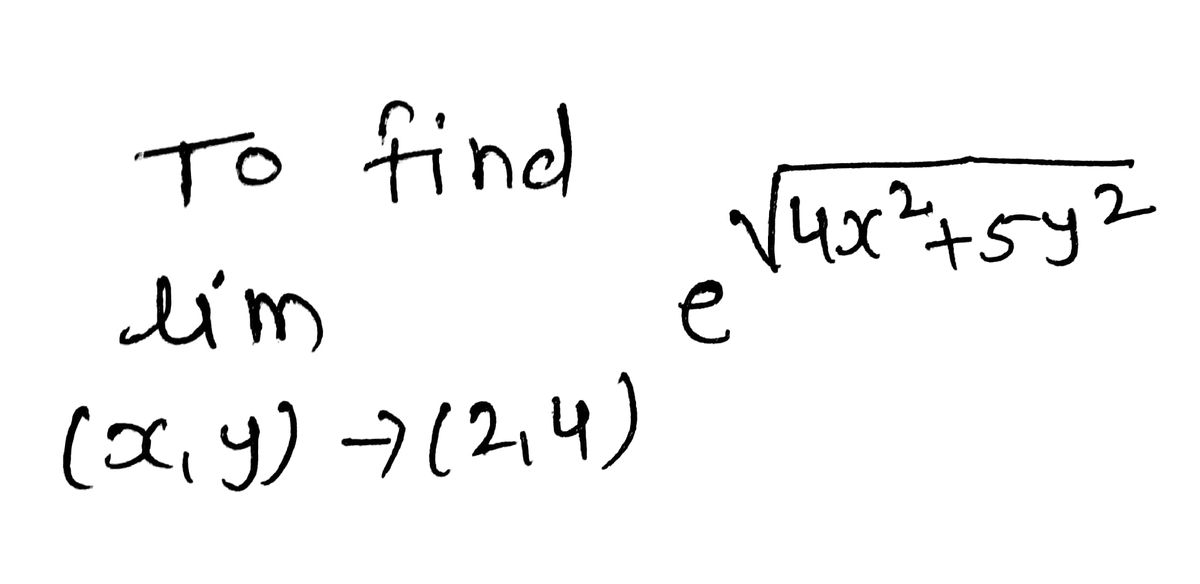
Step by step
Solved in 2 steps with 2 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

