Find the inverse of AB if 5 -4 A-¹ and B-1 = = (AB)-¹ = -2 -4 14 -5 2 ]
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
![**Topic: Matrix Inversion**
To find the inverse of the product \( AB \), we have the given inverses:
\[
A^{-1} =
\begin{bmatrix}
5 & -4 \\
-2 & -4
\end{bmatrix}
\]
and
\[
B^{-1} =
\begin{bmatrix}
1 & 4 \\
-5 & 2
\end{bmatrix}
\]
The formula for finding the inverse of the product \( AB \) is:
\[
(AB)^{-1} = B^{-1}A^{-1}
\]
To compute \( (AB)^{-1} \), multiply the matrices \( B^{-1} \) and \( A^{-1} \).
**Matrix Multiplication Steps:**
1. Multiply the first row of \( B^{-1} \) by the first column of \( A^{-1} \).
2. Multiply the first row of \( B^{-1} \) by the second column of \( A^{-1} \).
3. Multiply the second row of \( B^{-1} \) by the first column of \( A^{-1} \).
4. Multiply the second row of \( B^{-1} \) by the second column of \( A^{-1} \).
**Calculation:**
1. \( (1 \cdot 5) + (4 \cdot -2) \)
2. \( (1 \cdot -4) + (4 \cdot -4) \)
3. \( (-5 \cdot 5) + (2 \cdot -2) \)
4. \( (-5 \cdot -4) + (2 \cdot -4) \)
After performing these calculations, place the results in the corresponding positions of the \( 2 \times 2 \) matrix for \( (AB)^{-1} \).
**Conclusion:**
The inverse \( (AB)^{-1} \) matrix is:
\[
(AB)^{-1} =
\begin{bmatrix}
\text{[result 1]} & \text{[result 2]} \\
\text{[result 3]} & \text{[result 4]}
\end{bmatrix}
\]
---
This transcribed content can assist learners in understanding how to compute the inverse of a product of matrices step by step.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2Fb898cad9-5347-4e0a-a74d-32f84bfad0f6%2F555edcb5-4338-4369-8d37-7c720285ed4a%2Fnozox5b_processed.png&w=3840&q=75)
Transcribed Image Text:**Topic: Matrix Inversion**
To find the inverse of the product \( AB \), we have the given inverses:
\[
A^{-1} =
\begin{bmatrix}
5 & -4 \\
-2 & -4
\end{bmatrix}
\]
and
\[
B^{-1} =
\begin{bmatrix}
1 & 4 \\
-5 & 2
\end{bmatrix}
\]
The formula for finding the inverse of the product \( AB \) is:
\[
(AB)^{-1} = B^{-1}A^{-1}
\]
To compute \( (AB)^{-1} \), multiply the matrices \( B^{-1} \) and \( A^{-1} \).
**Matrix Multiplication Steps:**
1. Multiply the first row of \( B^{-1} \) by the first column of \( A^{-1} \).
2. Multiply the first row of \( B^{-1} \) by the second column of \( A^{-1} \).
3. Multiply the second row of \( B^{-1} \) by the first column of \( A^{-1} \).
4. Multiply the second row of \( B^{-1} \) by the second column of \( A^{-1} \).
**Calculation:**
1. \( (1 \cdot 5) + (4 \cdot -2) \)
2. \( (1 \cdot -4) + (4 \cdot -4) \)
3. \( (-5 \cdot 5) + (2 \cdot -2) \)
4. \( (-5 \cdot -4) + (2 \cdot -4) \)
After performing these calculations, place the results in the corresponding positions of the \( 2 \times 2 \) matrix for \( (AB)^{-1} \).
**Conclusion:**
The inverse \( (AB)^{-1} \) matrix is:
\[
(AB)^{-1} =
\begin{bmatrix}
\text{[result 1]} & \text{[result 2]} \\
\text{[result 3]} & \text{[result 4]}
\end{bmatrix}
\]
---
This transcribed content can assist learners in understanding how to compute the inverse of a product of matrices step by step.
Expert Solution
Step 1: Given part
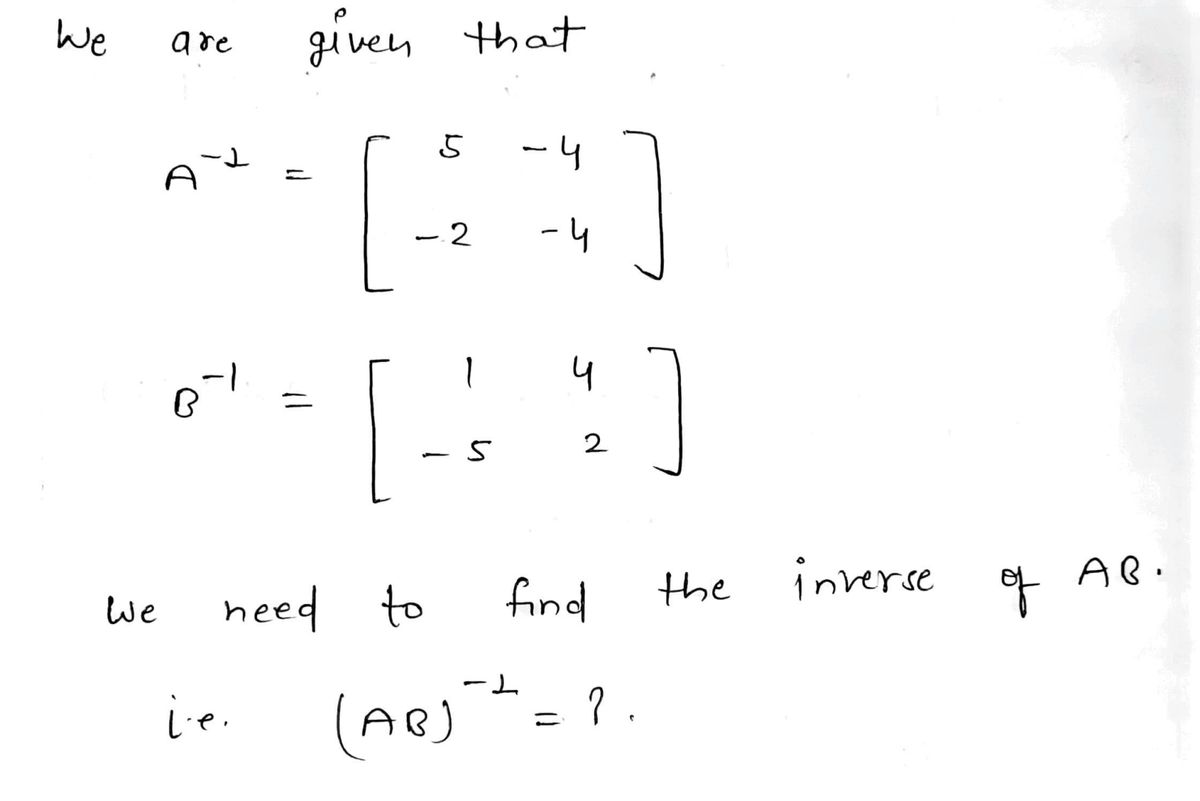
Step by step
Solved in 3 steps with 3 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

