Find the indicated partial derivatives by the method of implicit partial differentiation. dz 5xy +z*x- 3yz = 2; dx ... dz (Simplify your answer.) dx
Find the indicated partial derivatives by the method of implicit partial differentiation. dz 5xy +z*x- 3yz = 2; dx ... dz (Simplify your answer.) dx
Algebra and Trigonometry (6th Edition)
6th Edition
ISBN:9780134463216
Author:Robert F. Blitzer
Publisher:Robert F. Blitzer
ChapterP: Prerequisites: Fundamental Concepts Of Algebra
Section: Chapter Questions
Problem 1MCCP: In Exercises 1-25, simplify the given expression or perform the indicated operation (and simplify,...
Related questions
Question
2.
![**Problem Statement:**
Find the indicated partial derivatives by the method of implicit partial differentiation.
Given the equation:
\[ 5xy + z^4x - 3yz = 2 \]
Find \(\frac{\partial z}{\partial x}\).
**Solution:**
1. Differentiate both sides of the equation with respect to \( x \).
2. When differentiating terms involving \( z \), use the chain rule for implicit differentiation, treating \( z \) as a function of \( x \).
\[ \frac{\partial}{\partial x}(5xy + z^4x - 3yz) = \frac{\partial}{\partial x}(2) \]
- The derivative of \( 5xy \) with respect to \( x \) is \( 5y \).
- The derivative of \( z^4x \) with respect to \( x \) is \( z^4 + 4z^3x\frac{\partial z}{\partial x} \).
- The derivative of \(-3yz\) with respect to \( x \) is \(-3y\frac{\partial z}{\partial x}\).
- The derivative of 2 with respect to \( x \) is 0.
Now, solving the equation:
\[ 5y + z^4 + 4z^3x\frac{\partial z}{\partial x} - 3y\frac{\partial z}{\partial x} = 0 \]
Combine and solve for \(\frac{\partial z}{\partial x}\).
\[ 4z^3x\frac{\partial z}{\partial x} - 3y\frac{\partial z}{\partial x} = -5y - z^4 \]
Factor out \(\frac{\partial z}{\partial x}\).
\[ \frac{\partial z}{\partial x}(4z^3x - 3y) = -5y - z^4 \]
Finally, solve for \(\frac{\partial z}{\partial x}\).
\[ \frac{\partial z}{\partial x} = \frac{-5y - z^4}{4z^3x - 3y} \]
**(Simplify your answer.)**](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F55f0052a-9d0d-41a8-9339-203ce40e3605%2F12543127-a29f-4bfa-bf53-5ebfaed96728%2Fbnanpw7_processed.png&w=3840&q=75)
Transcribed Image Text:**Problem Statement:**
Find the indicated partial derivatives by the method of implicit partial differentiation.
Given the equation:
\[ 5xy + z^4x - 3yz = 2 \]
Find \(\frac{\partial z}{\partial x}\).
**Solution:**
1. Differentiate both sides of the equation with respect to \( x \).
2. When differentiating terms involving \( z \), use the chain rule for implicit differentiation, treating \( z \) as a function of \( x \).
\[ \frac{\partial}{\partial x}(5xy + z^4x - 3yz) = \frac{\partial}{\partial x}(2) \]
- The derivative of \( 5xy \) with respect to \( x \) is \( 5y \).
- The derivative of \( z^4x \) with respect to \( x \) is \( z^4 + 4z^3x\frac{\partial z}{\partial x} \).
- The derivative of \(-3yz\) with respect to \( x \) is \(-3y\frac{\partial z}{\partial x}\).
- The derivative of 2 with respect to \( x \) is 0.
Now, solving the equation:
\[ 5y + z^4 + 4z^3x\frac{\partial z}{\partial x} - 3y\frac{\partial z}{\partial x} = 0 \]
Combine and solve for \(\frac{\partial z}{\partial x}\).
\[ 4z^3x\frac{\partial z}{\partial x} - 3y\frac{\partial z}{\partial x} = -5y - z^4 \]
Factor out \(\frac{\partial z}{\partial x}\).
\[ \frac{\partial z}{\partial x}(4z^3x - 3y) = -5y - z^4 \]
Finally, solve for \(\frac{\partial z}{\partial x}\).
\[ \frac{\partial z}{\partial x} = \frac{-5y - z^4}{4z^3x - 3y} \]
**(Simplify your answer.)**
Expert Solution
Step 1
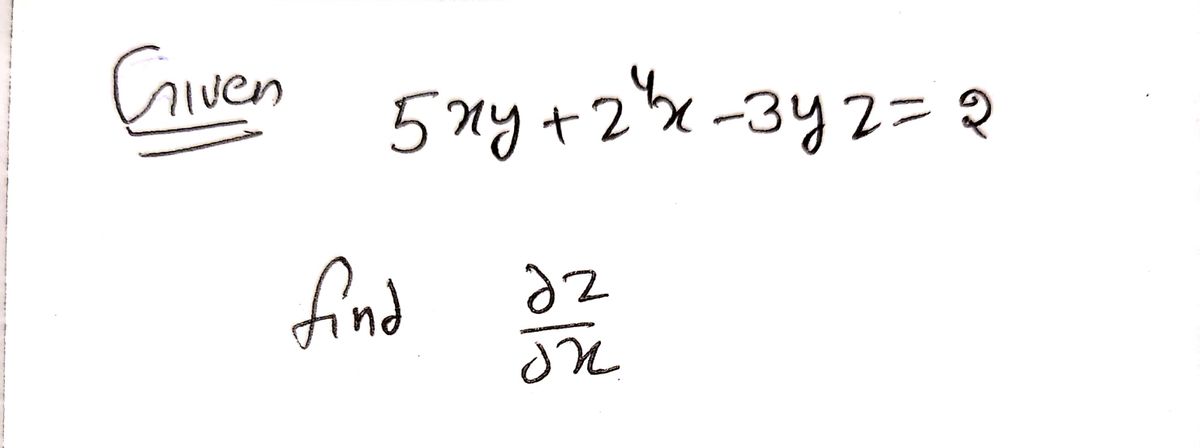
Step by step
Solved in 2 steps with 2 images

Recommended textbooks for you

Algebra and Trigonometry (6th Edition)
Algebra
ISBN:
9780134463216
Author:
Robert F. Blitzer
Publisher:
PEARSON

Contemporary Abstract Algebra
Algebra
ISBN:
9781305657960
Author:
Joseph Gallian
Publisher:
Cengage Learning

Linear Algebra: A Modern Introduction
Algebra
ISBN:
9781285463247
Author:
David Poole
Publisher:
Cengage Learning

Algebra and Trigonometry (6th Edition)
Algebra
ISBN:
9780134463216
Author:
Robert F. Blitzer
Publisher:
PEARSON

Contemporary Abstract Algebra
Algebra
ISBN:
9781305657960
Author:
Joseph Gallian
Publisher:
Cengage Learning

Linear Algebra: A Modern Introduction
Algebra
ISBN:
9781285463247
Author:
David Poole
Publisher:
Cengage Learning

Algebra And Trigonometry (11th Edition)
Algebra
ISBN:
9780135163078
Author:
Michael Sullivan
Publisher:
PEARSON

Introduction to Linear Algebra, Fifth Edition
Algebra
ISBN:
9780980232776
Author:
Gilbert Strang
Publisher:
Wellesley-Cambridge Press

College Algebra (Collegiate Math)
Algebra
ISBN:
9780077836344
Author:
Julie Miller, Donna Gerken
Publisher:
McGraw-Hill Education