Calculus: Early Transcendentals
8th Edition
ISBN:9781285741550
Author:James Stewart
Publisher:James Stewart
Chapter1: Functions And Models
Section: Chapter Questions
Problem 1RCC: (a) What is a function? What are its domain and range? (b) What is the graph of a function? (c) How...
Related questions
Question
Please give me a clean step-by-step answer. Thank you!
![**Problem:**
Find the exact value of the given expression.
\[ \tan\left(\frac{1}{2} \cos^{-1}\left(\frac{3}{4}\right)\right) \]
**Solution:**
To find the exact value of the expression, we first need to determine the angle \( \theta \) such that \( \cos(\theta) = \frac{3}{4} \). This angle is \(\cos^{-1}\left(\frac{3}{4}\right)\).
Then we apply the half-angle identity for tangent:
\[
\tan\left(\frac{\theta}{2}\right) = \pm \sqrt{\frac{1 - \cos(\theta)}{1 + \cos(\theta)}}
\]
In this case, \( \cos(\theta) = \frac{3}{4} \), so:
\[
\tan\left(\frac{\theta}{2}\right) = \pm \sqrt{\frac{1 - \frac{3}{4}}{1 + \frac{3}{4}}}
\]
\[
= \pm \sqrt{\frac{\frac{1}{4}}{\frac{7}{4}}}
\]
\[
= \pm \sqrt{\frac{1}{7}}
\]
Thus, the exact value of the expression is:
\[
\tan\left(\frac{1}{2} \cos^{-1}\left(\frac{3}{4}\right)\right) = \pm \sqrt{\frac{1}{7}}
\]
**Note:**
Since the context of the problem may indicate a specific quadrant, choose the appropriate sign (+ or -) based on the interval in which \(\frac{\theta}{2}\) lies.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F0ce77b62-15ca-430d-a006-9d8db870bed6%2Fbb7f86c4-a665-4d27-a9a0-433fe6518c7a%2Fbmegcyv_processed.png&w=3840&q=75)
Transcribed Image Text:**Problem:**
Find the exact value of the given expression.
\[ \tan\left(\frac{1}{2} \cos^{-1}\left(\frac{3}{4}\right)\right) \]
**Solution:**
To find the exact value of the expression, we first need to determine the angle \( \theta \) such that \( \cos(\theta) = \frac{3}{4} \). This angle is \(\cos^{-1}\left(\frac{3}{4}\right)\).
Then we apply the half-angle identity for tangent:
\[
\tan\left(\frac{\theta}{2}\right) = \pm \sqrt{\frac{1 - \cos(\theta)}{1 + \cos(\theta)}}
\]
In this case, \( \cos(\theta) = \frac{3}{4} \), so:
\[
\tan\left(\frac{\theta}{2}\right) = \pm \sqrt{\frac{1 - \frac{3}{4}}{1 + \frac{3}{4}}}
\]
\[
= \pm \sqrt{\frac{\frac{1}{4}}{\frac{7}{4}}}
\]
\[
= \pm \sqrt{\frac{1}{7}}
\]
Thus, the exact value of the expression is:
\[
\tan\left(\frac{1}{2} \cos^{-1}\left(\frac{3}{4}\right)\right) = \pm \sqrt{\frac{1}{7}}
\]
**Note:**
Since the context of the problem may indicate a specific quadrant, choose the appropriate sign (+ or -) based on the interval in which \(\frac{\theta}{2}\) lies.
![**Problem Statement:**
Find the exact value of the given expression.
\[
\tan\left(\frac{1}{2} \cos^{-1}\left(\frac{3}{4}\right)\right)
\]
**Description:**
This expression involves finding the tangent of half an angle, where the angle itself is determined by the inverse cosine (arccos) of \(\frac{3}{4}\). To solve this, you will first find the angle \(\theta\) such that \(\cos(\theta) = \frac{3}{4}\). Then, you calculate the tangent of \(\frac{\theta}{2}\).
**Instructions:**
1. Determine \(\theta\) such that \(\cos(\theta) = \frac{3}{4}\).
2. Use the identity for \(\tan\left(\frac{\theta}{2}\right)\):
\[
\tan\left(\frac{\theta}{2}\right) = \sqrt{\frac{1 - \cos(\theta)}{1 + \cos(\theta)}}
\]
3. Substitute \(\cos(\theta) = \frac{3}{4}\) into the identity and simplify.
4. Calculate the exact value.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F0ce77b62-15ca-430d-a006-9d8db870bed6%2Fbb7f86c4-a665-4d27-a9a0-433fe6518c7a%2Fxg1u4ko_processed.png&w=3840&q=75)
Transcribed Image Text:**Problem Statement:**
Find the exact value of the given expression.
\[
\tan\left(\frac{1}{2} \cos^{-1}\left(\frac{3}{4}\right)\right)
\]
**Description:**
This expression involves finding the tangent of half an angle, where the angle itself is determined by the inverse cosine (arccos) of \(\frac{3}{4}\). To solve this, you will first find the angle \(\theta\) such that \(\cos(\theta) = \frac{3}{4}\). Then, you calculate the tangent of \(\frac{\theta}{2}\).
**Instructions:**
1. Determine \(\theta\) such that \(\cos(\theta) = \frac{3}{4}\).
2. Use the identity for \(\tan\left(\frac{\theta}{2}\right)\):
\[
\tan\left(\frac{\theta}{2}\right) = \sqrt{\frac{1 - \cos(\theta)}{1 + \cos(\theta)}}
\]
3. Substitute \(\cos(\theta) = \frac{3}{4}\) into the identity and simplify.
4. Calculate the exact value.
Expert Solution
Step 1
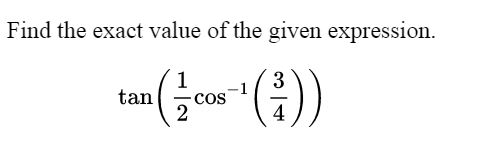
Step by step
Solved in 3 steps with 3 images

Recommended textbooks for you

Calculus: Early Transcendentals
Calculus
ISBN:
9781285741550
Author:
James Stewart
Publisher:
Cengage Learning

Thomas' Calculus (14th Edition)
Calculus
ISBN:
9780134438986
Author:
Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:
PEARSON

Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:
9780134763644
Author:
William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:
PEARSON

Calculus: Early Transcendentals
Calculus
ISBN:
9781285741550
Author:
James Stewart
Publisher:
Cengage Learning

Thomas' Calculus (14th Edition)
Calculus
ISBN:
9780134438986
Author:
Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:
PEARSON

Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:
9780134763644
Author:
William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:
PEARSON

Calculus: Early Transcendentals
Calculus
ISBN:
9781319050740
Author:
Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:
W. H. Freeman


Calculus: Early Transcendental Functions
Calculus
ISBN:
9781337552516
Author:
Ron Larson, Bruce H. Edwards
Publisher:
Cengage Learning