Find the equivalent resistance of five hundred 10 resistors when the resistors are connected in a. Series b. Parallel
Find the equivalent resistance of five hundred 10 resistors when the resistors are connected in a. Series b. Parallel
Related questions
Question
![**Calculating Equivalent Resistance**
Find the equivalent resistance of five hundred 10 Ω resistors when the resistors are connected in
a. **Series**
b. **Parallel**
---
**Explanation:**
- **Series Connection**: When resistors are connected in series, the equivalent resistance (\( R_{\text{eq}}\)) is the sum of all individual resistances. Therefore, the equivalent resistance for resistors in series is calculated as:
\[
R_{\text{eq(series)}} = R_1 + R_2 + R_3 + \ldots + R_n
\]
For 500 resistors, each with 10 Ω:
\[
R_{\text{eq(series)}} = 500 \times 10 \, \Omega = 5000 \, \Omega
\]
- **Parallel Connection**: When resistors are connected in parallel, the reciprocal of the equivalent resistance is the sum of the reciprocals of each individual resistance. Therefore, the equivalent resistance for resistors in parallel is calculated as:
\[
\frac{1}{R_{\text{eq(parallel)}}} = \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} + \ldots + \frac{1}{R_n}
\]
For 500 resistors, each with 10 Ω:
\[
\frac{1}{R_{\text{eq(parallel)}}} = 500 \times \frac{1}{10}
\]
\[
R_{\text{eq(parallel)}} = \frac{10}{500} \, \Omega = 0.02 \, \Omega
\]
This exercise provides insight into how the configuration of resistors in an electrical circuit affects the total equivalent resistance, thereby influencing the circuit's overall performance.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2Fb41c431a-d537-4c9f-b640-b49be1be5173%2F4134ca67-4734-4d77-b1f3-be36cd28c282%2Fnd6tl2j_processed.png&w=3840&q=75)
Transcribed Image Text:**Calculating Equivalent Resistance**
Find the equivalent resistance of five hundred 10 Ω resistors when the resistors are connected in
a. **Series**
b. **Parallel**
---
**Explanation:**
- **Series Connection**: When resistors are connected in series, the equivalent resistance (\( R_{\text{eq}}\)) is the sum of all individual resistances. Therefore, the equivalent resistance for resistors in series is calculated as:
\[
R_{\text{eq(series)}} = R_1 + R_2 + R_3 + \ldots + R_n
\]
For 500 resistors, each with 10 Ω:
\[
R_{\text{eq(series)}} = 500 \times 10 \, \Omega = 5000 \, \Omega
\]
- **Parallel Connection**: When resistors are connected in parallel, the reciprocal of the equivalent resistance is the sum of the reciprocals of each individual resistance. Therefore, the equivalent resistance for resistors in parallel is calculated as:
\[
\frac{1}{R_{\text{eq(parallel)}}} = \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} + \ldots + \frac{1}{R_n}
\]
For 500 resistors, each with 10 Ω:
\[
\frac{1}{R_{\text{eq(parallel)}}} = 500 \times \frac{1}{10}
\]
\[
R_{\text{eq(parallel)}} = \frac{10}{500} \, \Omega = 0.02 \, \Omega
\]
This exercise provides insight into how the configuration of resistors in an electrical circuit affects the total equivalent resistance, thereby influencing the circuit's overall performance.
Expert Solution
Step 1: Given data
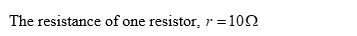
Step by step
Solved in 3 steps with 4 images
