Find the electric potential distribution of charged spherical surface with the charge q and the radius R
- Electric potential at a point in the field is defined as the work done in moving a unit positive test charge from infinity to that point against the electrostatic forces, along any path.
- Gauss's law states that the surface integral of electrostatic field produced by any sources over any closed surface S enclosing a volume V in vacuum is times the total charge (Q) contained inside S, i.e.,
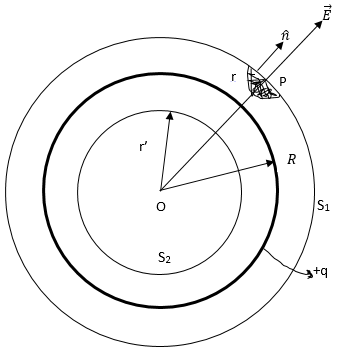
Let charge +q be distributed uniformly over the spherical surface.
To calculate electric field intensity at any point P, where OP=r, consider a sphere S1 with center O and radius r. This is a Gaussian surface, at every point of which is the same, directed radially outwards.
According to Gauss's theorem:
Clearly ,electric field intensity at any point outside the spherical surface is such, as if the entire charge was concentrated at the center of the spherical surface.
Potential outside the spherical surface is given by-
Potential at a point on the surface of the spherical surface is given by replacing r for R in the expression for electric potential outside the charged surface and is equal to
Now,
if the point P lies inside the spherical surface, then Gaussian surface is surface of a sphere S2 of radius r'<R. Since the charge enclosed by spherical surface is zero, therefore the Gaussian surface in this case encloses no charge, i.e.,
So potential at a point r' from the center of spherical surface is given as-
Step by step
Solved in 3 steps with 1 images









