Calculus: Early Transcendentals
8th Edition
ISBN:9781285741550
Author:James Stewart
Publisher:James Stewart
Chapter1: Functions And Models
Section: Chapter Questions
Problem 1RCC: (a) What is a function? What are its domain and range? (b) What is the graph of a function? (c) How...
Related questions
Question
![**Problem Statement:**
Find the derivative of the function.
Given:
\[ g(s) = 9s^2 - \frac{8}{s} + \frac{8}{\sqrt{s}} \]
Find:
\[ g'(s) = \, ? \]
**Instructions:**
- Differentiate each term of the function \( g(s) \) with respect to \( s \).
- Apply the power rule, quotient rule, and chain rule as needed.
**Steps to Consider:**
1. The first term \( 9s^2 \) can be differentiated using the power rule.
2. The second term \( \frac{8}{s} \) is equivalent to \( 8s^{-1} \) and can be differentiated using the power rule.
3. The third term \( \frac{8}{\sqrt{s}} \) is equivalent to \( 8s^{-\frac{1}{2}} \) and can also be differentiated using the power rule.
**Complete the calculation to find \( g'(s) \).**](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F87946fbe-26a8-44e7-b719-4f36f43dcbac%2Fc0db38a0-ec1e-42fc-a1bb-1ea4083b49c0%2Fruq7otx_processed.jpeg&w=3840&q=75)
Transcribed Image Text:**Problem Statement:**
Find the derivative of the function.
Given:
\[ g(s) = 9s^2 - \frac{8}{s} + \frac{8}{\sqrt{s}} \]
Find:
\[ g'(s) = \, ? \]
**Instructions:**
- Differentiate each term of the function \( g(s) \) with respect to \( s \).
- Apply the power rule, quotient rule, and chain rule as needed.
**Steps to Consider:**
1. The first term \( 9s^2 \) can be differentiated using the power rule.
2. The second term \( \frac{8}{s} \) is equivalent to \( 8s^{-1} \) and can be differentiated using the power rule.
3. The third term \( \frac{8}{\sqrt{s}} \) is equivalent to \( 8s^{-\frac{1}{2}} \) and can also be differentiated using the power rule.
**Complete the calculation to find \( g'(s) \).**
Expert Solution
Step 1
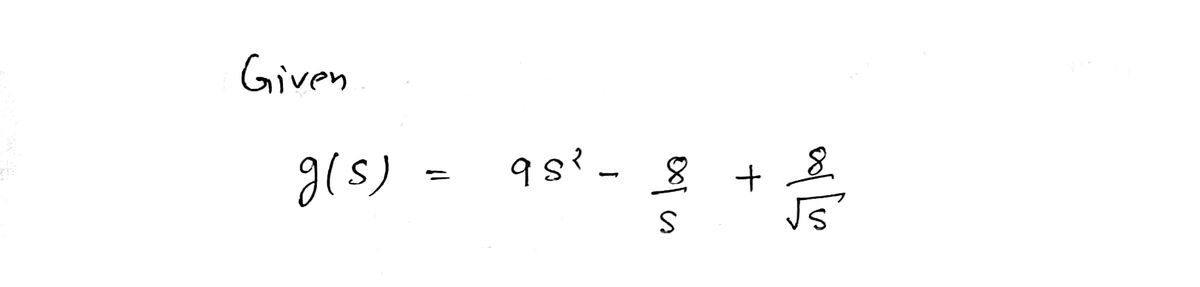
Step by step
Solved in 2 steps with 2 images

Recommended textbooks for you

Calculus: Early Transcendentals
Calculus
ISBN:
9781285741550
Author:
James Stewart
Publisher:
Cengage Learning

Thomas' Calculus (14th Edition)
Calculus
ISBN:
9780134438986
Author:
Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:
PEARSON

Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:
9780134763644
Author:
William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:
PEARSON

Calculus: Early Transcendentals
Calculus
ISBN:
9781285741550
Author:
James Stewart
Publisher:
Cengage Learning

Thomas' Calculus (14th Edition)
Calculus
ISBN:
9780134438986
Author:
Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:
PEARSON

Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:
9780134763644
Author:
William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:
PEARSON

Calculus: Early Transcendentals
Calculus
ISBN:
9781319050740
Author:
Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:
W. H. Freeman


Calculus: Early Transcendental Functions
Calculus
ISBN:
9781337552516
Author:
Ron Larson, Bruce H. Edwards
Publisher:
Cengage Learning