Find the connected components of each graph. (i) G=(V, E). V = {a, b, c, d, e}. E = 0 (ii) G=(V, E). V = {a, b, c, d, e, f}. E= {{c, f}, {a, b}, {d, a}, {e, c}, {b, f}} Determine the edge connectivity and the vertex connectivity of each graph. (i) (ii) 3 6 2 6 2 7 5 7 5 8 Figure 8: An undirected graph has 8 vertices, 1 through 8. 4 ver- tices form a rectangular shape in the center. Starting from the top left verter and moving clockwise, the vertices of the rectangular shape are, 3, 7, 5, and 6. Vertex 2 is at about the center of the rectangular shape. Vertex 8 is to the right of the rectangular shape. Vertex 1 and 4 are to the left of the rectangular shape, horizontally in-line with vertices 3 and 6, respectively. Undirected edges, line segments, are between the following vertices: 1 and 3; 3 and 7; 3 and 4; 3 and 6; 3 and 2; 4 and 2; 4 and 6; 6 and 2; 6 and 5; 2 and 5; 2 and 7; 2 and 8; 7 and 5; 7 and 8; and 5 and 8.
Ratios
A ratio is a comparison between two numbers of the same kind. It represents how many times one number contains another. It also represents how small or large one number is compared to the other.
Trigonometric Ratios
Trigonometric ratios give values of trigonometric functions. It always deals with triangles that have one angle measuring 90 degrees. These triangles are right-angled. We take the ratio of sides of these triangles.

(a)
We need to find the connected component of the following graph:
,
and
.
,
and
.
(b)
We need to find the edge connectivity and vertex connectivity of the following graph:
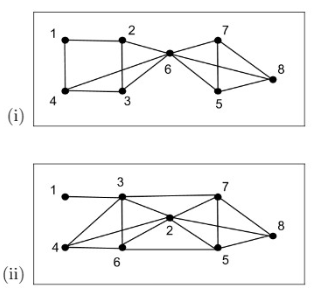
We know that the edge connectivity of a graph is the minimum number of edges, whose deletion from graph disconnects it.
The vertex connectivity of a graph is the minimum number of vertices, whose deletion from graph disconnects it.
Step by step
Solved in 5 steps with 41 images









