Find the area of one the graphs of bounded by cos Xe region Sinx and
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
#1
![**Problem 1:** Find the area of one region bounded by the graphs of \( \sin x \) and \( \cos x \).
**Problem 2:** Find the volume of the solid formed by revolving the region bounded by the graphs of:
\[ y = \sqrt{x} \]
\[ y = 0 \]
\[ x = 6 \]
**Graph/Diagram Explanation:**
- The first problem involves finding the area between the sine and cosine functions. Typically, this would involve identifying the points of intersection and setting up an integral to calculate the enclosed area.
- The second problem requires calculating the volume of a solid of revolution. The region under the curve \( y = \sqrt{x} \) from \( x = 0 \) to \( x = 6 \) is revolved around the x-axis, and the volume is found using the method of disks or washers.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2Fe35298e5-10ed-452c-b18c-35d9ef29ce25%2F459be4cf-f4ef-4089-9aa4-1a27ea39ba44%2Fhnbj44n_processed.jpeg&w=3840&q=75)
Transcribed Image Text:**Problem 1:** Find the area of one region bounded by the graphs of \( \sin x \) and \( \cos x \).
**Problem 2:** Find the volume of the solid formed by revolving the region bounded by the graphs of:
\[ y = \sqrt{x} \]
\[ y = 0 \]
\[ x = 6 \]
**Graph/Diagram Explanation:**
- The first problem involves finding the area between the sine and cosine functions. Typically, this would involve identifying the points of intersection and setting up an integral to calculate the enclosed area.
- The second problem requires calculating the volume of a solid of revolution. The region under the curve \( y = \sqrt{x} \) from \( x = 0 \) to \( x = 6 \) is revolved around the x-axis, and the volume is found using the method of disks or washers.
Expert Solution
Step 1
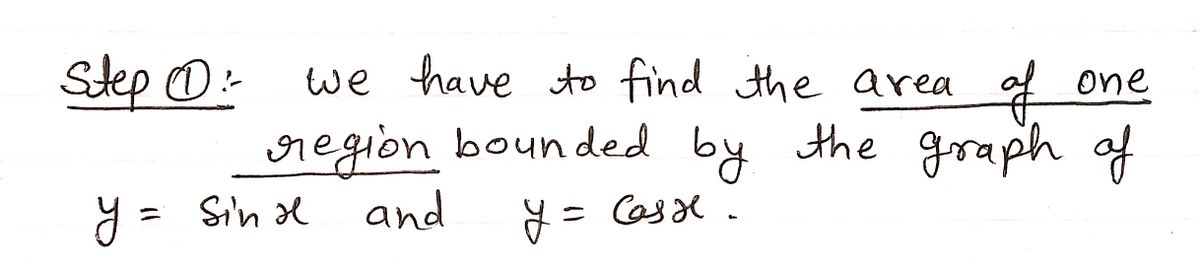
Step by step
Solved in 2 steps with 2 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

