Calculus: Early Transcendentals
8th Edition
ISBN:9781285741550
Author:James Stewart
Publisher:James Stewart
Chapter1: Functions And Models
Section: Chapter Questions
Problem 1RCC: (a) What is a function? What are its domain and range? (b) What is the graph of a function? (c) How...
Related questions
Question
![**Problem:**
Find the solution of the homogeneous linear ordinary differential equation (ODE):
\[
(D^2 + 6D + 13I)y = 0
\]
**Explanation:**
In this problem, \(D\) represents the differential operator, typically denoted as \(\frac{d}{dx}\), and \(I\) is the identity operator. The given ODE is a second-order homogeneous linear ODE. The task is to solve for \(y\), the function of \(x\) that satisfies this equation.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F99cc51a6-9278-4810-a568-442a3c7caa31%2F6f25d913-3436-4058-8089-9fc6ce19380c%2F8ix9ez_processed.jpeg&w=3840&q=75)
Transcribed Image Text:**Problem:**
Find the solution of the homogeneous linear ordinary differential equation (ODE):
\[
(D^2 + 6D + 13I)y = 0
\]
**Explanation:**
In this problem, \(D\) represents the differential operator, typically denoted as \(\frac{d}{dx}\), and \(I\) is the identity operator. The given ODE is a second-order homogeneous linear ODE. The task is to solve for \(y\), the function of \(x\) that satisfies this equation.
![### Problem 6
**Objective:** Find the solution of homogeneous linear ordinary differential equations (ODEs).
**Equation:**
\[
(D^2 - 5.5D + 6.66I)y = 0
\]
**Explanation:**
This problem involves solving a homogeneous linear ODE. The differential operator is given by \( D \), and the equation involves quadratic terms of the operator. The solution involves finding a function \( y \) such that the expression equals zero.
**Key Steps to Solve:**
1. **Characteristic Equation:** Set up the characteristic polynomial associated with the differential operator.
2. **Roots of the Polynomial:** Solve the polynomial to find the roots, which determine the general solution form.
3. **General Solution:** Use the roots to write down the solution, potentially involving exponential functions, depending on the nature (real or complex) of the roots.
This forms part of a broader study of differential equations, focusing on solutions where only the homogeneous part, associated with the differential operator, is addressed.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F99cc51a6-9278-4810-a568-442a3c7caa31%2F6f25d913-3436-4058-8089-9fc6ce19380c%2Frsbwpv_processed.jpeg&w=3840&q=75)
Transcribed Image Text:### Problem 6
**Objective:** Find the solution of homogeneous linear ordinary differential equations (ODEs).
**Equation:**
\[
(D^2 - 5.5D + 6.66I)y = 0
\]
**Explanation:**
This problem involves solving a homogeneous linear ODE. The differential operator is given by \( D \), and the equation involves quadratic terms of the operator. The solution involves finding a function \( y \) such that the expression equals zero.
**Key Steps to Solve:**
1. **Characteristic Equation:** Set up the characteristic polynomial associated with the differential operator.
2. **Roots of the Polynomial:** Solve the polynomial to find the roots, which determine the general solution form.
3. **General Solution:** Use the roots to write down the solution, potentially involving exponential functions, depending on the nature (real or complex) of the roots.
This forms part of a broader study of differential equations, focusing on solutions where only the homogeneous part, associated with the differential operator, is addressed.
Expert Solution
Step 1
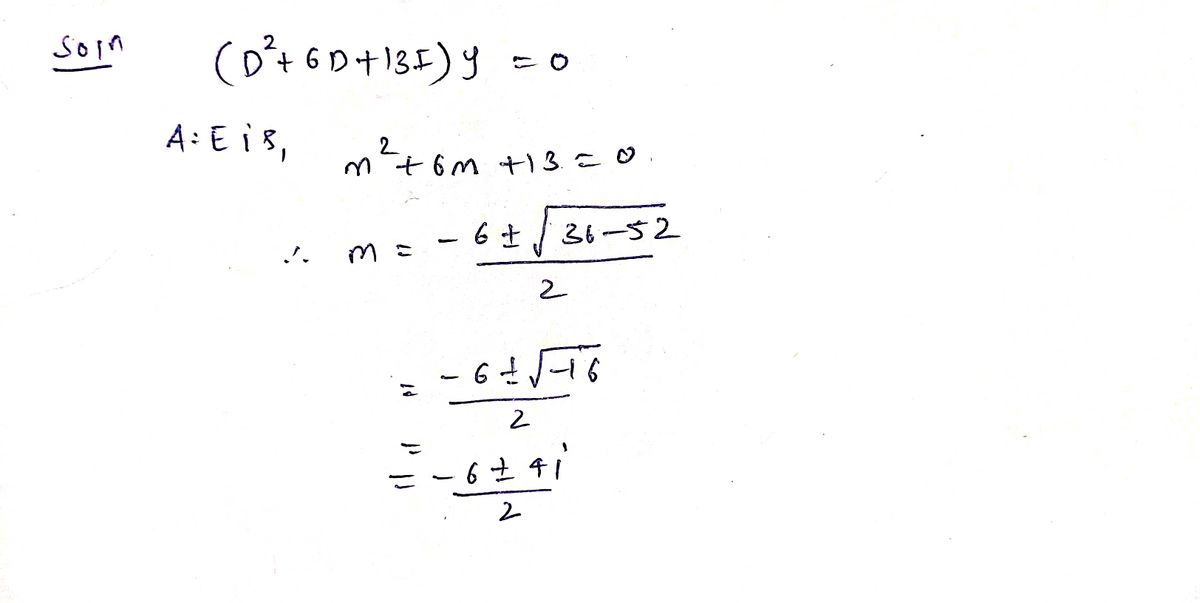
Step by step
Solved in 2 steps with 2 images

Recommended textbooks for you

Calculus: Early Transcendentals
Calculus
ISBN:
9781285741550
Author:
James Stewart
Publisher:
Cengage Learning

Thomas' Calculus (14th Edition)
Calculus
ISBN:
9780134438986
Author:
Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:
PEARSON

Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:
9780134763644
Author:
William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:
PEARSON

Calculus: Early Transcendentals
Calculus
ISBN:
9781285741550
Author:
James Stewart
Publisher:
Cengage Learning

Thomas' Calculus (14th Edition)
Calculus
ISBN:
9780134438986
Author:
Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:
PEARSON

Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:
9780134763644
Author:
William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:
PEARSON

Calculus: Early Transcendentals
Calculus
ISBN:
9781319050740
Author:
Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:
W. H. Freeman


Calculus: Early Transcendental Functions
Calculus
ISBN:
9781337552516
Author:
Ron Larson, Bruce H. Edwards
Publisher:
Cengage Learning