Find an equation of the tangent line to the graph of the function at the point (1, 1). y = x cosh(x) y = Need Help? Read It Master It
Find an equation of the tangent line to the graph of the function at the point (1, 1). y = x cosh(x) y = Need Help? Read It Master It
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
![**Problem Statement:**
Find an equation of the tangent line to the graph of the function at the point (1, 1).
**Function:**
\[ y = x^{\cosh(x)} \]
**Solution Box:**
\[ y = \, \text{[Input Field]} \]
**Additional Resources:**
- **Need Help?**
- [Read It](#)
- [Master It](#)
**Explanation for Students:**
The task is to find the equation of the tangent line for the provided function at a specific point. The given function involves the hyperbolic cosine function, \( \cosh(x) \). To solve this, you'll need to:
1. Differentiate the function to find the derivative, which gives the slope of the tangent line.
2. Evaluate the derivative at the given point to find the slope at that specific point.
3. Use the point-slope form of a line to write the equation of the tangent line.
If you need assistance with these steps, use the resources provided by clicking on "Read It" for a detailed explanation or "Master It" for practice problems.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F99ab9443-d48f-4a7b-b5cc-19d2edf5b7f5%2Fb264d556-21df-416c-8458-0af0611ce17f%2F19oc19_processed.jpeg&w=3840&q=75)
Transcribed Image Text:**Problem Statement:**
Find an equation of the tangent line to the graph of the function at the point (1, 1).
**Function:**
\[ y = x^{\cosh(x)} \]
**Solution Box:**
\[ y = \, \text{[Input Field]} \]
**Additional Resources:**
- **Need Help?**
- [Read It](#)
- [Master It](#)
**Explanation for Students:**
The task is to find the equation of the tangent line for the provided function at a specific point. The given function involves the hyperbolic cosine function, \( \cosh(x) \). To solve this, you'll need to:
1. Differentiate the function to find the derivative, which gives the slope of the tangent line.
2. Evaluate the derivative at the given point to find the slope at that specific point.
3. Use the point-slope form of a line to write the equation of the tangent line.
If you need assistance with these steps, use the resources provided by clicking on "Read It" for a detailed explanation or "Master It" for practice problems.
Expert Solution
Formula for tangent line
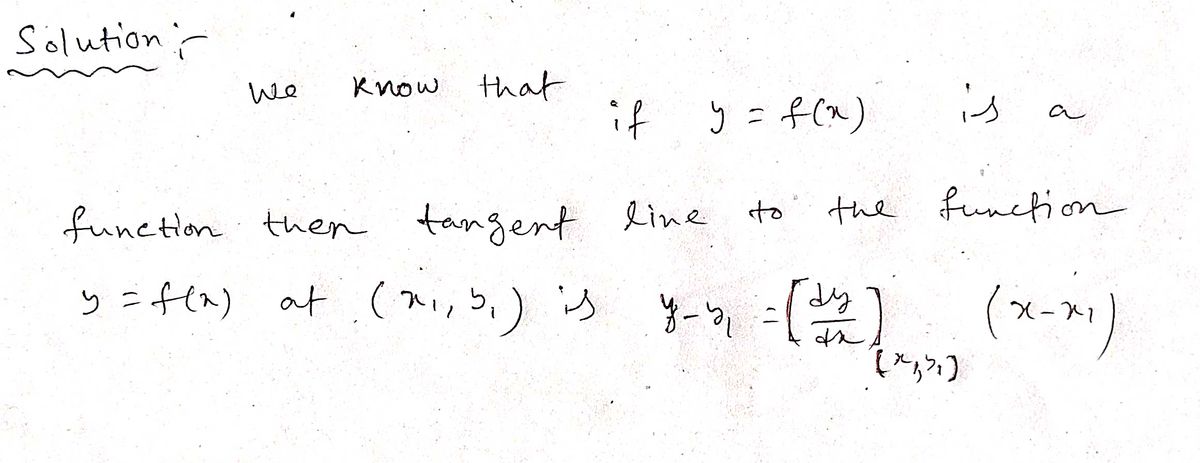
Step by step
Solved in 2 steps with 2 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

