Algebra and Trigonometry (6th Edition)
6th Edition
ISBN:9780134463216
Author:Robert F. Blitzer
Publisher:Robert F. Blitzer
ChapterP: Prerequisites: Fundamental Concepts Of Algebra
Section: Chapter Questions
Problem 1MCCP: In Exercises 1-25, simplify the given expression or perform the indicated operation (and simplify,...
Related questions
Question
100%
![**Problem Statement:**
**Objective:**
Find the equation of a line that passes through the point \((2, 3)\) and is perpendicular to the line represented by the equation \(y = 2x - 7\).
**Solution:**
To solve this problem, follow these steps:
1. **Identify the Slope of the Given Line:**
- The line's equation is \(y = 2x - 7\).
- The slope (m) of this line is 2.
2. **Determine the Slope of the Perpendicular Line:**
- The slope of a line that is perpendicular to another is the negative reciprocal of the original slope.
- Therefore, the slope of the perpendicular line is \(-\frac{1}{2}\).
3. **Use the Point-Slope Form to Find the Equation:**
- The point-slope form of a line is given by \(y - y_1 = m(x - x_1)\), where \((x_1, y_1)\) is a point on the line, and \(m\) is the slope.
- Substitute \((x_1, y_1) = (2, 3)\) and \(m = -\frac{1}{2}\) into the formula:
\[
y - 3 = -\frac{1}{2}(x - 2)
\]
4. **Simplify the Equation:**
- Distribute the slope on the right-hand side:
\[
y - 3 = -\frac{1}{2}x + 1
\]
- Add 3 to both sides to solve for \(y\):
\[
y = -\frac{1}{2}x + 4
\]
**Conclusion:**
The equation of the line that passes through the point \((2, 3)\) and is perpendicular to the line \(y = 2x - 7\) is:
\[ y = -\frac{1}{2}x + 4 \]](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F543c40ca-509d-4a54-93c4-2ee368b8fc52%2Ffd38c817-381c-4537-a5a1-1fc0905226dc%2Fll3wd9f_processed.jpeg&w=3840&q=75)
Transcribed Image Text:**Problem Statement:**
**Objective:**
Find the equation of a line that passes through the point \((2, 3)\) and is perpendicular to the line represented by the equation \(y = 2x - 7\).
**Solution:**
To solve this problem, follow these steps:
1. **Identify the Slope of the Given Line:**
- The line's equation is \(y = 2x - 7\).
- The slope (m) of this line is 2.
2. **Determine the Slope of the Perpendicular Line:**
- The slope of a line that is perpendicular to another is the negative reciprocal of the original slope.
- Therefore, the slope of the perpendicular line is \(-\frac{1}{2}\).
3. **Use the Point-Slope Form to Find the Equation:**
- The point-slope form of a line is given by \(y - y_1 = m(x - x_1)\), where \((x_1, y_1)\) is a point on the line, and \(m\) is the slope.
- Substitute \((x_1, y_1) = (2, 3)\) and \(m = -\frac{1}{2}\) into the formula:
\[
y - 3 = -\frac{1}{2}(x - 2)
\]
4. **Simplify the Equation:**
- Distribute the slope on the right-hand side:
\[
y - 3 = -\frac{1}{2}x + 1
\]
- Add 3 to both sides to solve for \(y\):
\[
y = -\frac{1}{2}x + 4
\]
**Conclusion:**
The equation of the line that passes through the point \((2, 3)\) and is perpendicular to the line \(y = 2x - 7\) is:
\[ y = -\frac{1}{2}x + 4 \]
Expert Solution
Step 1
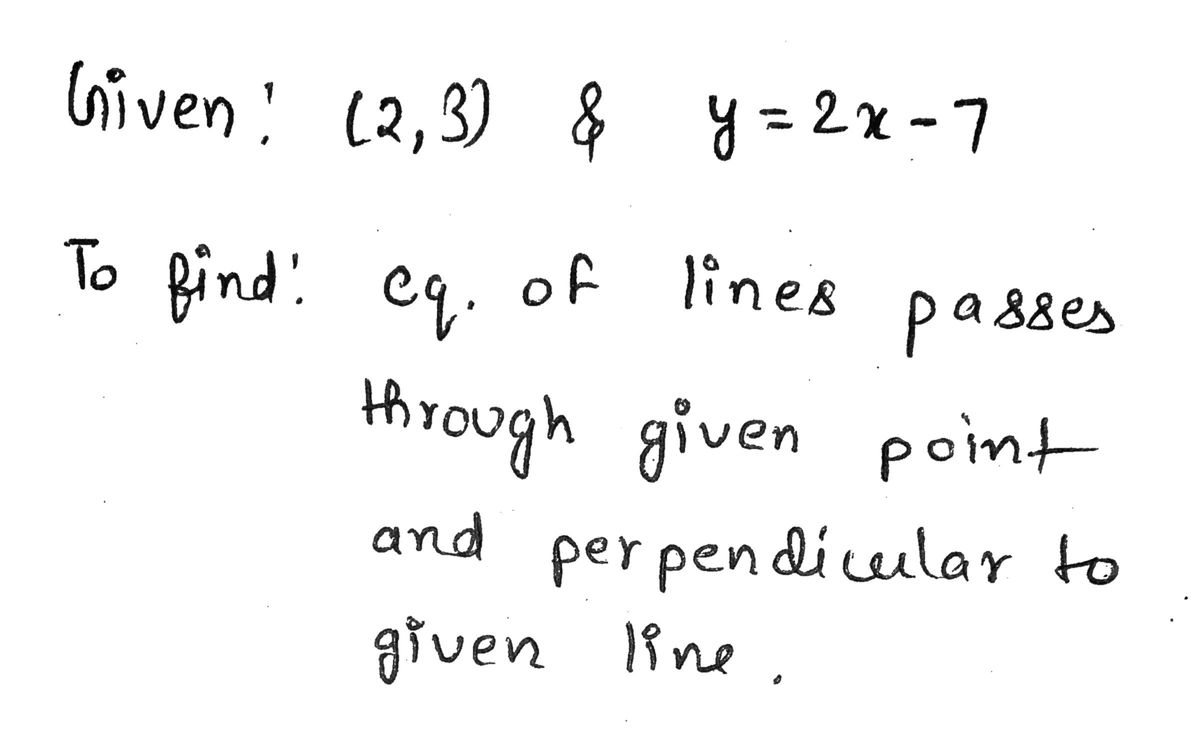
Step by step
Solved in 2 steps with 2 images

Recommended textbooks for you

Algebra and Trigonometry (6th Edition)
Algebra
ISBN:
9780134463216
Author:
Robert F. Blitzer
Publisher:
PEARSON

Contemporary Abstract Algebra
Algebra
ISBN:
9781305657960
Author:
Joseph Gallian
Publisher:
Cengage Learning

Linear Algebra: A Modern Introduction
Algebra
ISBN:
9781285463247
Author:
David Poole
Publisher:
Cengage Learning

Algebra and Trigonometry (6th Edition)
Algebra
ISBN:
9780134463216
Author:
Robert F. Blitzer
Publisher:
PEARSON

Contemporary Abstract Algebra
Algebra
ISBN:
9781305657960
Author:
Joseph Gallian
Publisher:
Cengage Learning

Linear Algebra: A Modern Introduction
Algebra
ISBN:
9781285463247
Author:
David Poole
Publisher:
Cengage Learning

Algebra And Trigonometry (11th Edition)
Algebra
ISBN:
9780135163078
Author:
Michael Sullivan
Publisher:
PEARSON

Introduction to Linear Algebra, Fifth Edition
Algebra
ISBN:
9780980232776
Author:
Gilbert Strang
Publisher:
Wellesley-Cambridge Press

College Algebra (Collegiate Math)
Algebra
ISBN:
9780077836344
Author:
Julie Miller, Donna Gerken
Publisher:
McGraw-Hill Education