Find all strings in L((a + b) b (a + ab)*) of length less than four.

Finite state machine(FSM) is the simplest way of finding the strings from the given language, L. Finite state machine has the fundamental utility of recognizing the patterns in the language. FSM allows into it, the string of symbol as an input and turns its state as per the functionality. If a desired symbol is arrives as an input, then the transition occurs. A transition in the automata may take it to another next state or may have the same state.
FSM facilitates two types of states:
- Accept state, if the input string of the language, L is successfully processed and the machine reaches to its final state successfully.
- Reject state, if the input string ends on a non final state. In this case the input string doesn't belong to the language, L, hence is rejected.
FSM consists of:
Q: refers to the finite set of states{q0,q1,q2 and q3}
∑: is the finite set of input symbols{a,b}
q0: it is the initial state in the machine
F: it is the final state in the machine
δ: it refers to the transition function(defined as δ: Q x ∑ →Q )
For the L=((a+b)b(a+ab)*), corresponding Finite State Machine is shown in Figure 1:
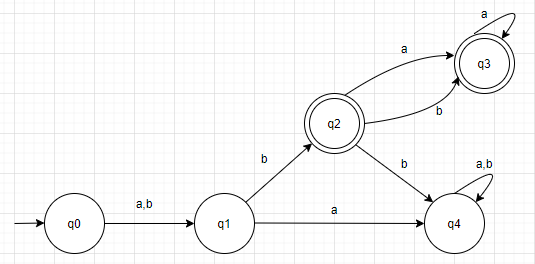
Figure 1
Trending now
This is a popular solution!
Step by step
Solved in 2 steps with 1 images









