Find a linear differential operator that annihilates the given function. (Use D for the differential operator.) 2 + ex cos 4x
Find a linear differential operator that annihilates the given function. (Use D for the differential operator.) 2 + ex cos 4x
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
![**Problem Statement:**
Find a linear differential operator that annihilates the given function. (Use \(D\) for the differential operator.)
\[ 2 + e^x \cos 4x \]
**Explanation:**
You are asked to determine a differential operator using \(D\) (where \(D\) represents differentiation with respect to \(x\)) that, when applied to the function \(2 + e^x \cos 4x\), results in zero.
The function is composed of:
1. A constant term \(2\).
2. A composite function \(e^x \cos 4x\), which involves an exponential function and a trigonometric function.
The process involves finding an operator that accounts for the characteristics of these components, particularly focusing on differential operations that involve exponential and trigonometric terms.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F25fce74d-50ce-4010-8593-c528dce466b9%2F6047554f-af73-49a4-a7a9-0eadbb53d77e%2F4pkgt1o_processed.png&w=3840&q=75)
Transcribed Image Text:**Problem Statement:**
Find a linear differential operator that annihilates the given function. (Use \(D\) for the differential operator.)
\[ 2 + e^x \cos 4x \]
**Explanation:**
You are asked to determine a differential operator using \(D\) (where \(D\) represents differentiation with respect to \(x\)) that, when applied to the function \(2 + e^x \cos 4x\), results in zero.
The function is composed of:
1. A constant term \(2\).
2. A composite function \(e^x \cos 4x\), which involves an exponential function and a trigonometric function.
The process involves finding an operator that accounts for the characteristics of these components, particularly focusing on differential operations that involve exponential and trigonometric terms.
Expert Solution
Step 1
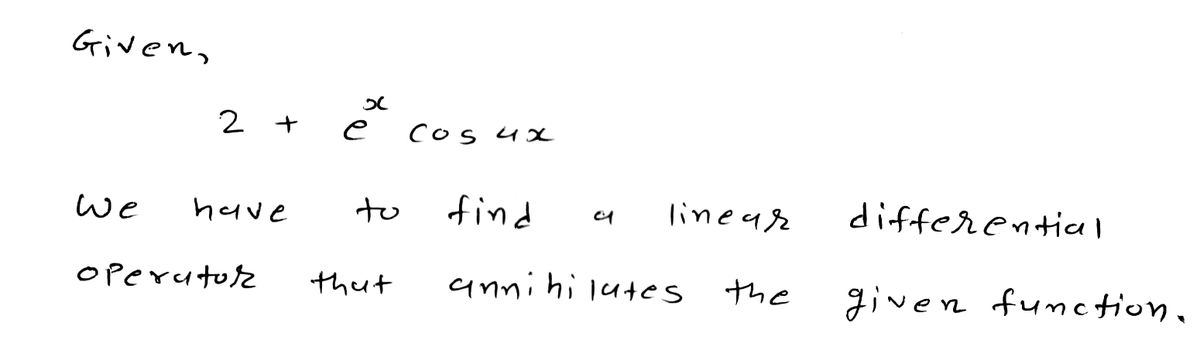
Step by step
Solved in 3 steps with 3 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

