Find 1 3 2 + 9 4 + (−1)26 226 326
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
![**Problem Statement:**
Find the sum of the series:
\[ 1 - \frac{3}{2} + \frac{9}{4} - \cdots + (-1)^{26} \frac{3^{26}}{2^{26}}. \]
**Instructions:**
1. Identify the pattern within the series.
2. Determine the type of series and derive the formula for the sum.
3. Calculate the sum of the series using the derived formula.
**Explanation:**
This series can be recognized as a geometric series where each term involves a power of \(\frac{3}{2}\) and alternates sign. Note the alternating signs are facilitated by \((-1)^n\) where \(n\) is even for this specific sum.
To find the sum of this series:
- **Common Ratio (\(r\))**: \(-\frac{3}{2}\)
- **First Term (\(a\))**: \(1\)
The sum \(S_n\) of the first \(n\) terms of a geometric series can be calculated using the formula:
\[ S_n = a \frac{1 - r^n}{1 - r} \]
For this problem, \(n = 26\).
Proceed by applying this formula to find the sum of the series.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F9ff37d99-6df7-4773-b15e-140cb7fb42c8%2F5fd366b5-9136-4951-9bab-a8d49da98975%2F7gjufe4_processed.png&w=3840&q=75)
Transcribed Image Text:**Problem Statement:**
Find the sum of the series:
\[ 1 - \frac{3}{2} + \frac{9}{4} - \cdots + (-1)^{26} \frac{3^{26}}{2^{26}}. \]
**Instructions:**
1. Identify the pattern within the series.
2. Determine the type of series and derive the formula for the sum.
3. Calculate the sum of the series using the derived formula.
**Explanation:**
This series can be recognized as a geometric series where each term involves a power of \(\frac{3}{2}\) and alternates sign. Note the alternating signs are facilitated by \((-1)^n\) where \(n\) is even for this specific sum.
To find the sum of this series:
- **Common Ratio (\(r\))**: \(-\frac{3}{2}\)
- **First Term (\(a\))**: \(1\)
The sum \(S_n\) of the first \(n\) terms of a geometric series can be calculated using the formula:
\[ S_n = a \frac{1 - r^n}{1 - r} \]
For this problem, \(n = 26\).
Proceed by applying this formula to find the sum of the series.
Expert Solution
Step 1: Finding the pattern
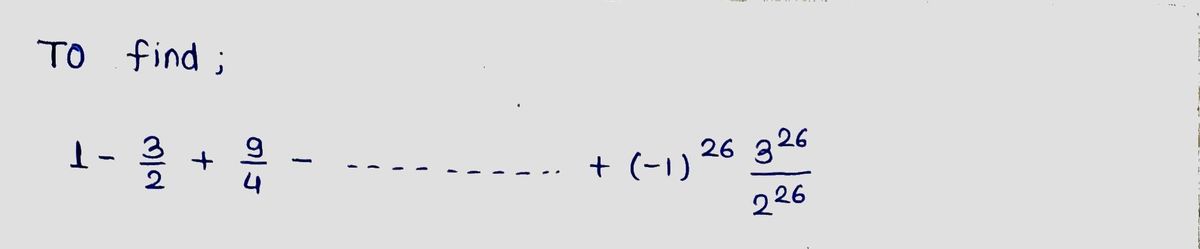
Step by step
Solved in 3 steps with 3 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

