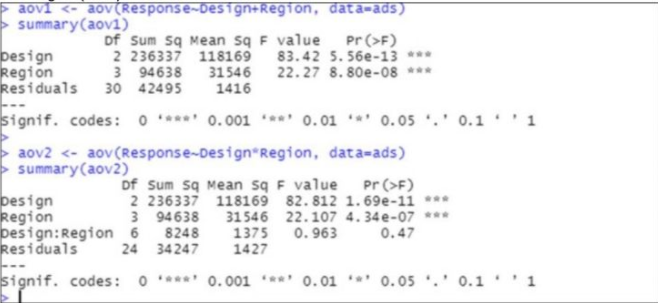
Figure 1 shows the results of the statistical test without interaction term between Region and Design (aov1), and the statistical test with interaction term betweenRegion and Design (aov2) as R output for this problem.Figure 1.R output of model results for two statistical models, one without an interaction term between Design and Region (aov1) and one with interaction term between Designand Region (aov2).aovi <- aov(Response-Design+Region, data=ads)summary(aov1)þesignRegionResidualsDf Sum Sq Mean sq F value2 2363373 9463830118169315461416Pr (>F)83.42 5.56e-13 ***22.27 8. 80e-08 ***42495signif. codes: 0 ****' 0.001 ***' 0.01 **' 0.05 '.' 0.1 ''1aov2 <- aov(Response-Design*Region, data=ads)summary(aov2)of Sum sq Mean sq F value2 236337 118169 82. 812 1.69e-11 ***Pr (>F)þesignRegionþesign:Region 6Residuals3 9463882483424731546 22.107 4. 34e-07 ***0. 963137514270.4724---signif. codes:O ***0.0010. 01 *0.05 .' 0.1'1Using a significant at the significance level alpha = 0.05, based on Figure 1 which statement is correct?%DThe model without interaction (aov1) shows that the factors Design and Region are not significant with regards to their impact on survey responses at the selectedsignificance level.The model with interaction (aov2) shows that interaction term between Design and Region is significant with regards to the impact on survey responses at theselected significance level.Using the model with interaction (aov2) results, we fail to reject the null hypothesis related to interaction between Design and Region at the selected significancelevel, i.e., we can't reject that the levels of Design are the same with regards to the impact of Region on Response, and we can't reject that levels of Region arethe same with regards to the impact of Design on Response.Using the model with interaction (aov2) results, we reject the null hypothesis related to interaction between Design and Region at the selected significance level,i.e., we reject that the levels of Design are the same with regards to the impact of Region on Response, and we reject that levels of Region are the same withregards to the impact of Design on Response.

Answered: Figure 1 shows the results of the…

MATLAB: An Introduction with Applications

6th Edition

ISBN:9781119256830

Author:Amos Gilat

Publisher:Amos Gilat

Chapter1: Starting With Matlab

Section: Chapter Questions

Problem 1P

See similar textbooks

Similar questions

Define the Distributed Lag Model with Additional Lags and AR(p) Errors?
Psychologists have identified 20 clients, 10 women and 10 men, and divided them into groups of five to determine the effect of matching the sex of the client and the sex of the therapist on the number of activities of daily living (ad1) performed by depressed clients. (a) Identify one of the independent variables. (b) Identify the other independent variable. (c) identify the dependent variable. (d) Using SPSS test all main and interaction effects at the .05 level of significance. Create a table including the cell means and marginal means and label each variable and level. State your null decision and conclusion (step 5 hypothesis testing) for all main and interaction effects. Label each effect clearly. Report in APA format the F statistics for all main and interaction effects. Be sure to report the best p-value possible.
The CSV file modeldata.csv contains 200 observations of 4 explanatory variables (x1, x2, x3, x4) and a response variable (y). A multiple linear regression model is built in R using the following code, > modeldata <- read.csv("modeldata.csv") > x1 <- modeldata$x1 > x2 <- modeldata$x2 > x3 <- modeldata$x3 > x4 <- modeldata$x4 > y <- modeldata$y > model <- lm(y~x1+x2+x3+x4) Question: What this particular plot shows about the model being analysed?
What measures of fit are typically used to assess binary dependent variableregression models?
The CSV file modeldata.csv contains 200 observations of 4 explanatory variables (x1, x2, x3, x4) and a response variable (y). A multiple linear regression model is built in R using the following code, > modeldata <- read.csv("modeldata.csv") > x1 <- modeldata$x1 > x2 <- modeldata$x2 > x3 <- modeldata$x3 > x4 <- modeldata$x4 > y <- modeldata$y > model <- lm(y~x1+x2+x3+x4) Question: What this particular plot shows about the model being analysed?
Explain why it can be dangerous to use the least-squares line to obtain predictions for x values that are substantially larger or smaller than those contained in the sample. The least-squares line is based on the x values ---Select--- ✓the sample. We do not know that the same linear relationship will apply for x values ---Select--- the range of values in the sample. Therefore the least-squares line should not be used for x values ---Select--- the range of values in the sample.
Suppose a professor wants to know how the time spent studying affects student performance on microeconomic exams in college. She uses her class as a convenience sample, and she implements a randomized controlled trial by randomly dividing her class into a treatment and a control group to answer this question. Her experimental data contains the number of hours students study per week and their final microeconomics exam scores. If she estimates the following bivariate model using OLS, will her estimates of beta0 and beta1 be unbiased? Why or why not? examscore_i=beta0+beta1*hrsstudy_i+u_i No, because exam scores are unlikely to be normally distributed. Yes, because she conducted a randomized controlled trial. Yes, because there are unlikely to be outlier observations in exam scores or hours spent studying. No, because she didn't collect a random sample from the population of interest. No, because there is likely no relationship between study time and exam scores. Yes, because the OLS…
Perform an independent-sample t-test in SPSS to determine if the diet type (Variable 'diet'- diet type: meat eater and vegetarian) influence the pulse rate when running (Variable 'stage 3'-pulse running). Specifically, you want to know whether meat eaters have significantly higher pulse rate (stage 3: pulse running) than vegetarians. Use α = .05 The dependent variable is
Do i need to manually add time dummy variables when using proc panel in SAS? Or does it automatically account for it? For example, assuming a balanced equation, if my population model is y_it = alpha_t + x1_it + x2_it + c_i + u_it; where alpha_t is our our time dummy variables for each time period.

Recommended textbooks for you

MATLAB: An Introduction with Applications

Statistics

ISBN:

9781119256830

Author:

Amos Gilat

Publisher:

John Wiley & Sons Inc

Probability and Statistics for Engineering and th…

Statistics

ISBN:

9781305251809

Author:

Jay L. Devore

Publisher:

Cengage Learning

Statistics for The Behavioral Sciences (MindTap C…

Statistics

ISBN:

9781305504912

Author:

Frederick J Gravetter, Larry B. Wallnau

Publisher:

Cengage Learning

MATLAB: An Introduction with Applications

Statistics

ISBN:

9781119256830

Author:

Amos Gilat

Publisher:

John Wiley & Sons Inc

Probability and Statistics for Engineering and th…

Statistics

ISBN:

9781305251809

Author:

Jay L. Devore

Publisher:

Cengage Learning

Statistics for The Behavioral Sciences (MindTap C…

Statistics

ISBN:

9781305504912

Author:

Frederick J Gravetter, Larry B. Wallnau

Publisher:

Cengage Learning

Elementary Statistics: Picturing the World (7th E…

Statistics

ISBN:

9780134683416

Author:

Ron Larson, Betsy Farber

Publisher:

PEARSON

The Basic Practice of Statistics

Statistics

ISBN:

9781319042578

Author:

David S. Moore, William I. Notz, Michael A. Fligner

Publisher:

W. H. Freeman

Introduction to the Practice of Statistics

Statistics

ISBN:

9781319013387

Author:

David S. Moore, George P. McCabe, Bruce A. Craig

Publisher:

W. H. Freeman

SEE MORE TEXTBOOKS