Federal law under Title 49 of the United States Code, Chapter 301, Motor Vehicle Safety Standard took
Compound Probability
Compound probability can be defined as the probability of the two events which are independent. It can be defined as the multiplication of the probability of two events that are not dependent.
Tree diagram
Probability theory is a branch of mathematics that deals with the subject of probability. Although there are many different concepts of probability, probability theory expresses the definition mathematically through a series of axioms. Usually, these axioms express probability in terms of a probability space, which assigns a measure with values ranging from 0 to 1 to a set of outcomes known as the sample space. An event is a subset of these outcomes that is described.
Conditional Probability
By definition, the term probability is expressed as a part of mathematics where the chance of an event that may either occur or not is evaluated and expressed in numerical terms. The range of the value within which probability can be expressed is between 0 and 1. The higher the chance of an event occurring, the closer is its value to be 1. If the probability of an event is 1, it means that the event will happen under all considered circumstances. Similarly, if the probability is exactly 0, then no matter the situation, the event will never occur.
- Federal law under Title 49 of the United States Code, Chapter 301, Motor Vehicle Safety Standard took effect on January 1, 1968 and required all vehicles (except buses) to be fitted with seat belts in all designated seating positions. While most states have laws requiring seat belt use today, some people still do not “buckle up.” Let’s assume that 90 % of drivers do “buckle up.” If drivers are randomly stopped to check seat belt usage, answer the following questions and show your work.
- How many drivers do they expect to stop before finding a driver whose seatbelt is not buckled?
- What is the
probability that the second unbelted driver is in the ninth car stopped?
- What is the probability that of the first 10 drivers, 8 or more are wearing their seatbelts?
Given that 90% of drivers buckled up(wear seat belt).
The percentage of drivers without seat belt is,= 100%-90%=10%=10/100=0.10
Let the random variable x be the number of cars stopped to get the first driver without Seat belt.
The probability of success is considered as the percentage of drivers without seat belt. That is, p= 0.10
Here x follows geometric distribution with parameter p=0.10.
Therefore, the expected number of drivers to stop before finding a driver whose seatbelt is not buckled is ,
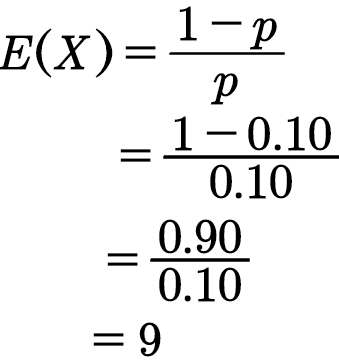
Trending now
This is a popular solution!
Step by step
Solved in 3 steps with 3 images









