Investigate the asymptotic behavior of ?(?)=4?2?2+1 numerically, computing the values of the function for ?=±50, ±100, ±500, and ±1000. (Use decimal notation. Give your answers to six decimal places.) ?(−50)= ?(50)= ?(−100)= ?(100)= ?(−500)= ?(500)= ?(−1000)= ?(1000)= Graph ?(?) using the graphing utility. ?(?)= What are the horizontal asymptotes of ?? (Give your answer as a comma‑separated list of equations. Express numbers in exact form. Use symbolic notation and fractions where
Investigate the asymptotic behavior of ?(?)=4?2?2+1 numerically, computing the values of the function for ?=±50, ±100, ±500, and ±1000. (Use decimal notation. Give your answers to six decimal places.) ?(−50)= ?(50)= ?(−100)= ?(100)= ?(−500)= ?(500)= ?(−1000)= ?(1000)= Graph ?(?) using the graphing utility. ?(?)= What are the horizontal asymptotes of ?? (Give your answer as a comma‑separated list of equations. Express numbers in exact form. Use symbolic notation and fractions where
Calculus: Early Transcendentals
8th Edition
ISBN:9781285741550
Author:James Stewart
Publisher:James Stewart
Chapter1: Functions And Models
Section: Chapter Questions
Problem 1RCC: (a) What is a function? What are its domain and range? (b) What is the graph of a function? (c) How...
Related questions
Question
Investigate the asymptotic behavior of ?(?)=4?2?2+1 numerically, computing the values of the function for ?=±50, ±100, ±500, and ±1000.
(Use decimal notation. Give your answers to six decimal places.)
?(−50)=
?(50)=
?(−100)=
?(100)=
?(−500)=
?(500)=
?(−1000)=
?(1000)=
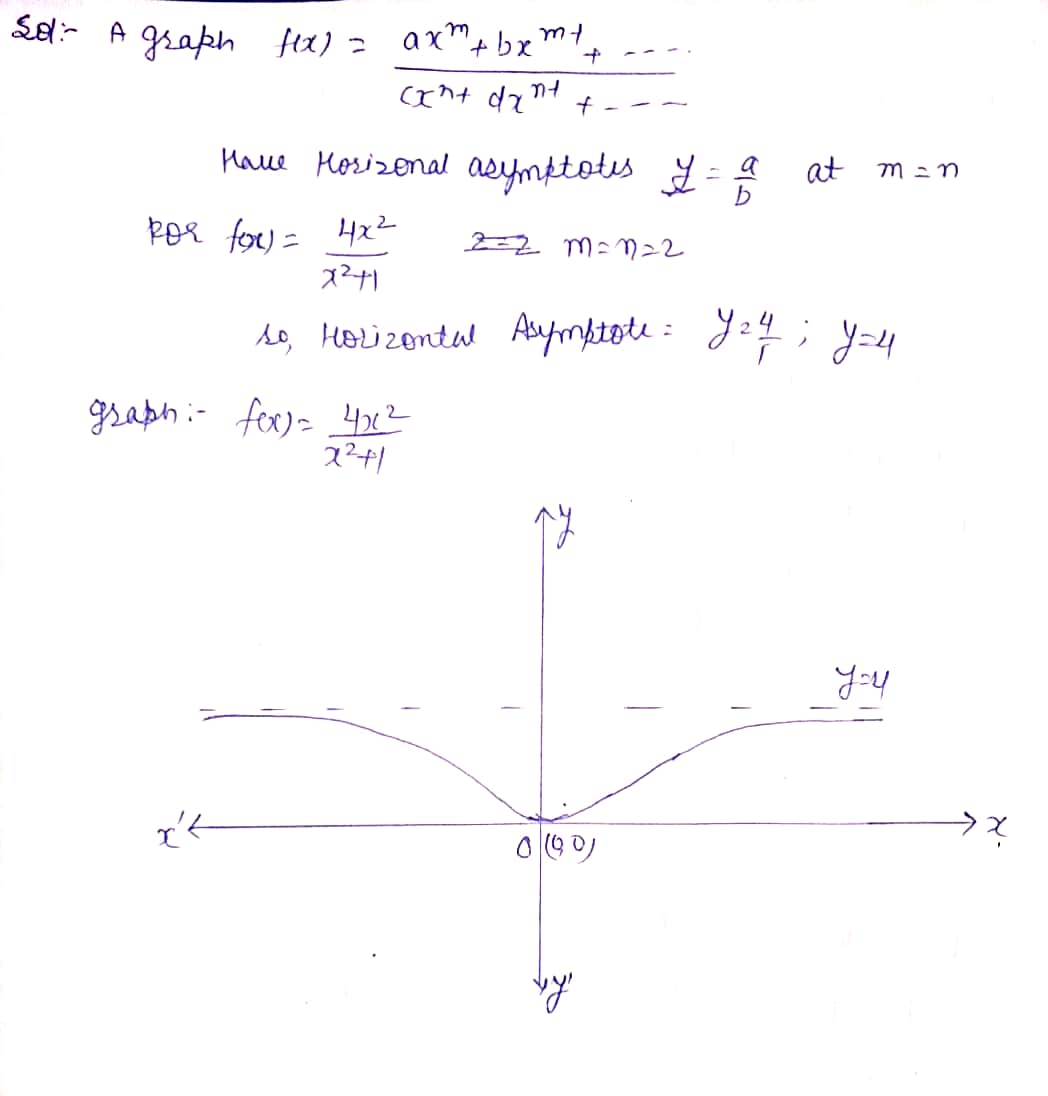
Graph ?(?) using the graphing utility.
?(?)=
What are the horizontal asymptotes of ??
(Give your answer as a comma‑separated list of equations. Express numbers in exact form. Use symbolic notation and fractions where needed.)
horizontal asymptote(s):

Transcribed Image Text:2 of 19 >
f(-500)=
f(500)=
f(-1000) =
f(1000) =
Graph f(x) using the graphing utility.
f(x) =
Question Source: Rogawski 4e Calculus Early Transcendentals Publisher: W.H. Fr

Transcribed Image Text:f(-50)=
Investigate the asymptotic behavior of f(x) =
+500, and ±1000.
(Use decimal notation. Give your answers to six decimal places.)
f(50) =
f(-100) =
4x²
x² +1
f(100) =
numerically, computing the values of the function for x = ±50, ±100,
Question Source: Rogawski 4e Calculus Early Transcendentals | Publisher: W.H. Fre
Expert Solution
Step 1
Step by step
Solved in 2 steps with 2 images

Follow-up Questions
Read through expert solutions to related follow-up questions below.
Follow-up Question
Investigate the limit numerically and graphically.
lim?→±∞8?+14?2+9‾‾‾‾‾‾‾‾√limx→±∞8x+14x2+9
Calculate the values of ?(?)=8?+14?2+9‾‾‾‾‾‾‾‾√f(x)=8x+14x2+9 for ?=±100,x=±100, ±500,±500, ±1000,±1000, and ±10000.and ±10000.
(Use decimal notation. Give your answers to six decimal places.)
?(−100)=f(−100)=
?(−500)=f(−500)=
?(−1000)=f(−1000)=
?(−10000)=f(−10000)=
?(100)=f(100)=
?(500)=f(500)=
?(1000)=f(1000)=
?(10000)=f(10000)=
Graph ?(?)f(x) using the graphing utility.
?(?)=f(x)=
8x+1√4x2+9
powered by
What are the horizontal asymptotes of ??of f?
(Give your answer as a comma‑separated list of equations. Express numbers in exact form. Use symbolic notation and fractions where needed.)
horizontal asymptote(s):
Transcribed Image Text:f(500) =
f(1000) =
f(10000) =
Graph f(x) using the graphing utility.
f(x) =
-10
8x + 1
√4x² +9
-5
y
horizontal asymptote(s):
-6
-3-
-9
9
6
CO
-3-
5
+
●
10
x
powered by
desmos
What are the horizontal asymptotes of f?
(Give your answer as a comma-separated list of equations. Express numbers in exact form. Use symbolic notation and fractions
where needed.)
Transcribed Image Text:SEP
18
Q
F4
Investigate the limit numerically and graphically.
8x + 1
lim
x-100 √√4x² +9
8x + 1
√4x²+9
(Use decimal notation. Give your answers to six decimal places.)
Calculate the values of f(x) =
%
f(-100) =
f(-500) =
f(-1000) =
f(-10000): =
f(100) =
f(500):
=
C
9
F5
tv ♫
C
F6
@
for x = ±100, +500, 1000, and +10000.
NT
"
F7
الله
DII
F8
A
S
F9
จ
Question Source: Rogawski 4e Calculus Eam
F10
V
Solution
Follow-up Question
Investigate the asymptotic behavior of ?(?)=4?2?2+1f(x)=4x2x2+1 numerically, computing the values of the function for ?=±50,x=±50, ±100,±100, ±500,±500, and ±1000.and ±1000.
(Use decimal notation. Give your answers to six decimal places.)
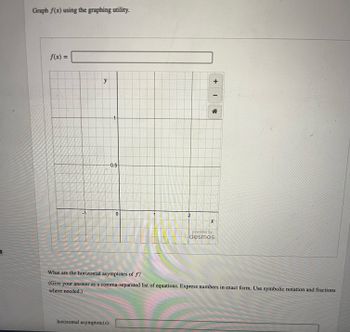
Transcribed Image Text:Graph f(x) using the graphing utility.
f(x) =
-1
3
y
-1
-0.5
horizontal asymptote(s):
0
2
+
x
powered by
desmos
What are the horizontal asymptotes of f?
(Give your answer as a comma-separated list of equations. Express numbers in exact form. Use symbolic notation and fractions
where needed.)

Transcribed Image Text:4x²
x² + 1
numerically, computing the values of the function for x = ±50, +100,
Investigate the asymptotic behavior of ƒ(x) =
+500, and ±1000.
(Use decimal notation. Give your answers to six decimal places.)
Solution
Recommended textbooks for you

Calculus: Early Transcendentals
Calculus
ISBN:
9781285741550
Author:
James Stewart
Publisher:
Cengage Learning

Thomas' Calculus (14th Edition)
Calculus
ISBN:
9780134438986
Author:
Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:
PEARSON

Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:
9780134763644
Author:
William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:
PEARSON

Calculus: Early Transcendentals
Calculus
ISBN:
9781285741550
Author:
James Stewart
Publisher:
Cengage Learning

Thomas' Calculus (14th Edition)
Calculus
ISBN:
9780134438986
Author:
Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:
PEARSON

Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:
9780134763644
Author:
William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:
PEARSON

Calculus: Early Transcendentals
Calculus
ISBN:
9781319050740
Author:
Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:
W. H. Freeman


Calculus: Early Transcendental Functions
Calculus
ISBN:
9781337552516
Author:
Ron Larson, Bruce H. Edwards
Publisher:
Cengage Learning