f ** Let f E C[0, 1] be given by f(x) = e". For each n 2 0, let fn E C0, 1] be given by 7L fn(x) = T=0 (so fn(x) is the first n+1 terms in the Maclaurin Series expansion of e"). Show that the sequence (fn) converges to f. (Use the Lo metric.)
f ** Let f E C[0, 1] be given by f(x) = e". For each n 2 0, let fn E C0, 1] be given by 7L fn(x) = T=0 (so fn(x) is the first n+1 terms in the Maclaurin Series expansion of e"). Show that the sequence (fn) converges to f. (Use the Lo metric.)
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
![** Let f e C(0, 1] be given by f(x) = e². For each n > 0, let fn E C[0, 1] be
given by
72
Σ
fn(T) =
r!
T=0
(so fn(r) is the first n +1 terms in the Maclaurin Series expansion of e"). Show
that the sequence (fn) converges to f. (Use the L metric.)](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2Fead15ed3-ba6a-41c2-9d2a-a187cc2ccb25%2F6c7e216b-b807-45ea-b33d-ed944d514ad3%2Ffpvtlb_processed.jpeg&w=3840&q=75)
Transcribed Image Text:** Let f e C(0, 1] be given by f(x) = e². For each n > 0, let fn E C[0, 1] be
given by
72
Σ
fn(T) =
r!
T=0
(so fn(r) is the first n +1 terms in the Maclaurin Series expansion of e"). Show
that the sequence (fn) converges to f. (Use the L metric.)
Expert Solution
Step 1
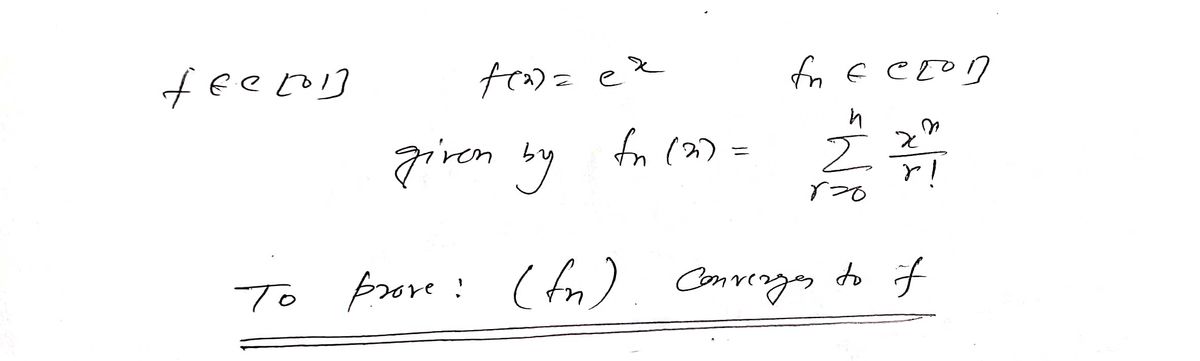
Step by step
Solved in 2 steps with 2 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

