(f + g)(x) use the given: f(x) (f- g)(-5) = 5x+1 2 x -9 and g(x) = (f. g)(0) 4x-2 2 x -9 to evaluate: — (x)
(f + g)(x) use the given: f(x) (f- g)(-5) = 5x+1 2 x -9 and g(x) = (f. g)(0) 4x-2 2 x -9 to evaluate: — (x)
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
![### Problem Statement
Given the functions:
\[ f(x) = \frac{5x + 1}{x^2 - 9} \]
\[ g(x) = \frac{4x - 2}{x^2 - 9} \]
Evaluate the following:
1. \((f + g)(x)\)
2. \((f - g)(-5)\)
3. \((f \cdot g)(0)\)
4. \(\frac{f}{g}(x)\)
### Detailed Explanation
To solve these problems, we'll use the definitions and operations of functions:
1. **Addition of Functions \((f + g)(x)\):**
\[
(f + g)(x) = f(x) + g(x) = \frac{5x + 1}{x^2 - 9} + \frac{4x - 2}{x^2 - 9}
\]
Since the denominators are the same, we can combine the numerators:
\[
(f + g)(x) = \frac{(5x + 1) + (4x - 2)}{x^2 - 9} = \frac{9x - 1}{x^2 - 9}
\]
2. **Subtraction of Functions \((f - g)(-5)\):**
Evaluate \(f(-5)\) and \(g(-5)\):
\[
f(-5) = \frac{5(-5) + 1}{(-5)^2 - 9} = \frac{-25 + 1}{25 - 9} = \frac{-24}{16} = -\frac{3}{2}
\]
\[
g(-5) = \frac{4(-5) - 2}{(-5)^2 - 9} = \frac{-20 - 2}{25 - 9} = \frac{-22}{16} = -\frac{11}{8}
\]
Subtract them:
\[
(f - g)(-5) = f(-5) - g(-5) = -\frac{3}{2} + \frac{11}{8} = -\frac{12}{8} + \frac{11}{8} = -\frac{1}{8}](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F1bafa714-33cc-47c4-a9a5-96cfac78ec18%2Fbe843d8d-1352-4b9b-b0c1-1e6b47d8f004%2Fhynlei_processed.jpeg&w=3840&q=75)
Transcribed Image Text:### Problem Statement
Given the functions:
\[ f(x) = \frac{5x + 1}{x^2 - 9} \]
\[ g(x) = \frac{4x - 2}{x^2 - 9} \]
Evaluate the following:
1. \((f + g)(x)\)
2. \((f - g)(-5)\)
3. \((f \cdot g)(0)\)
4. \(\frac{f}{g}(x)\)
### Detailed Explanation
To solve these problems, we'll use the definitions and operations of functions:
1. **Addition of Functions \((f + g)(x)\):**
\[
(f + g)(x) = f(x) + g(x) = \frac{5x + 1}{x^2 - 9} + \frac{4x - 2}{x^2 - 9}
\]
Since the denominators are the same, we can combine the numerators:
\[
(f + g)(x) = \frac{(5x + 1) + (4x - 2)}{x^2 - 9} = \frac{9x - 1}{x^2 - 9}
\]
2. **Subtraction of Functions \((f - g)(-5)\):**
Evaluate \(f(-5)\) and \(g(-5)\):
\[
f(-5) = \frac{5(-5) + 1}{(-5)^2 - 9} = \frac{-25 + 1}{25 - 9} = \frac{-24}{16} = -\frac{3}{2}
\]
\[
g(-5) = \frac{4(-5) - 2}{(-5)^2 - 9} = \frac{-20 - 2}{25 - 9} = \frac{-22}{16} = -\frac{11}{8}
\]
Subtract them:
\[
(f - g)(-5) = f(-5) - g(-5) = -\frac{3}{2} + \frac{11}{8} = -\frac{12}{8} + \frac{11}{8} = -\frac{1}{8}
Expert Solution
Step 1: Given
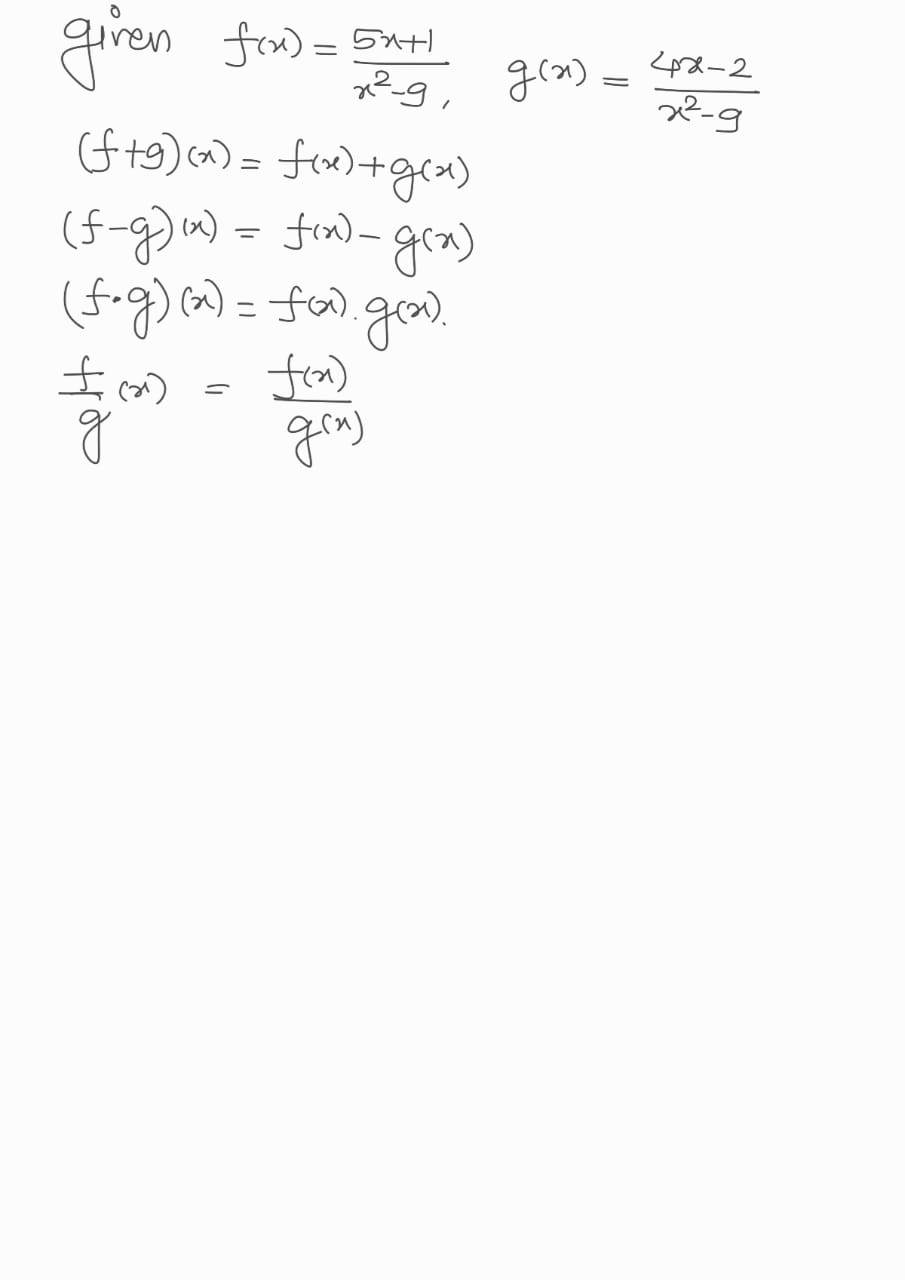
Step by step
Solved in 4 steps with 4 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

