Explain why a polynomial of degree 3 has at least one root. Start by examining the end-behavior of a polynomial of degree 3. Which statement correctly describes the end-behavior of a polynomial of degree 3? OA If f(x) has a leading term of ax, then lim f(x) = lim f(x) = b for some real number b. X00 X - 00 OR If f(x) has a leading term of ax, then either lim f(x) = 00 and lim f(x) = - o when a>0 or lim f(x) = - 00 and lim f(x) = 00 when a <0. X00 X- 00 X00 X - 00 Oc If f(x) has a leading term of ax, then either lim f(x) = 00 and lim f(x) = 00 when a>0 or lim f(x) = - 00 and lim f(x) = - 00 when a <0. X- 00 X00 X - 00 Which statement correctly concludes that f has at least one root? O A. Since fis a continuous function and the limits at infinity are both finite values, the intermediate-value theorem guarantees that f(R) = (-b, b) for some real number b and, hence, f has at least one root. O B. Since fis a continuous function and the limits at infinity have opposite signs, the intermediate-value theorem guarantees that f(R) =R and, hence, f has at least one root. O C. Since fis a continuous function and the limits at infinity have the same sign, the intermediate-value theorem guarantees that f(R) = [0, 00) or f(R) = (- 00, 0] and, hence, f has at least one root.
Explain why a polynomial of degree 3 has at least one root. Start by examining the end-behavior of a polynomial of degree 3. Which statement correctly describes the end-behavior of a polynomial of degree 3? OA If f(x) has a leading term of ax, then lim f(x) = lim f(x) = b for some real number b. X00 X - 00 OR If f(x) has a leading term of ax, then either lim f(x) = 00 and lim f(x) = - o when a>0 or lim f(x) = - 00 and lim f(x) = 00 when a <0. X00 X- 00 X00 X - 00 Oc If f(x) has a leading term of ax, then either lim f(x) = 00 and lim f(x) = 00 when a>0 or lim f(x) = - 00 and lim f(x) = - 00 when a <0. X- 00 X00 X - 00 Which statement correctly concludes that f has at least one root? O A. Since fis a continuous function and the limits at infinity are both finite values, the intermediate-value theorem guarantees that f(R) = (-b, b) for some real number b and, hence, f has at least one root. O B. Since fis a continuous function and the limits at infinity have opposite signs, the intermediate-value theorem guarantees that f(R) =R and, hence, f has at least one root. O C. Since fis a continuous function and the limits at infinity have the same sign, the intermediate-value theorem guarantees that f(R) = [0, 00) or f(R) = (- 00, 0] and, hence, f has at least one root.
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Concept explainers
Angles in Circles
Angles within a circle are feasible to create with the help of different properties of the circle such as radii, tangents, and chords. The radius is the distance from the center of the circle to the circumference of the circle. A tangent is a line made perpendicular to the radius through its endpoint placed on the circle as well as the line drawn at right angles to a tangent across the point of contact when the circle passes through the center of the circle. The chord is a line segment with its endpoints on the circle. A secant line or secant is the infinite extension of the chord.
Arcs in Circles
A circular arc is the arc of a circle formed by two distinct points. It is a section or segment of the circumference of a circle. A straight line passing through the center connecting the two distinct ends of the arc is termed a semi-circular arc.
Topic Video
Question
1-13)
![Explain why a polynomial of degree 3 has at least one root.
Start by examining the end-behavior of a polynomial of degree 3. Which statement correctly describes the end-behavior of a polynomial of degree 3?
OA If f(x) has a leading term of ax, then lim f(x) = lim f(x) = b for some real number b.
X00
X - 00
OP If f(x) has a leading term of ax, then either lim f(x) = 00 and lim f(x) = - 0 when a>0 or lim f(x) = - 0o and lim f(x) = oo when a <0.
X00
X - 00
X00
X - 00
Oc If f(x) has a leading term of ax, then either lim f(x) = 00 and
lim f(x) = 00 when a>0 or lim f(x) = - 00 and
lim f(x) = - oo when a <0.
X00
X - 00
X00
X - 00
Which statement correctly concludes that f has at least one root?
O A. Since fis a continuous function and the limits at infinity are both finite values, the intermediate-value theorem guarantees that f(R) = (- b, b) for some real number b and, hence, f has at least one root.
O B. Since fis a continuous function and the limits at infinity have opposite signs, the intermediate-value theorem guarantees that f(R) = R and, hence, f has at least one root.
O C. Since fis a continuous function and the limits at infinity have the same sign, the intermediate-value theorem guarantees that f(R) = [0, 00) or f(R) = (- 00, 0] and, hence, f has at least one root.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2Fb4e8e2a5-a7b3-45d7-b3fc-bbdb74e12e7d%2Fdfe4bbf0-e919-43f3-a3eb-b788298f117e%2Fy6skn0i_processed.png&w=3840&q=75)
Transcribed Image Text:Explain why a polynomial of degree 3 has at least one root.
Start by examining the end-behavior of a polynomial of degree 3. Which statement correctly describes the end-behavior of a polynomial of degree 3?
OA If f(x) has a leading term of ax, then lim f(x) = lim f(x) = b for some real number b.
X00
X - 00
OP If f(x) has a leading term of ax, then either lim f(x) = 00 and lim f(x) = - 0 when a>0 or lim f(x) = - 0o and lim f(x) = oo when a <0.
X00
X - 00
X00
X - 00
Oc If f(x) has a leading term of ax, then either lim f(x) = 00 and
lim f(x) = 00 when a>0 or lim f(x) = - 00 and
lim f(x) = - oo when a <0.
X00
X - 00
X00
X - 00
Which statement correctly concludes that f has at least one root?
O A. Since fis a continuous function and the limits at infinity are both finite values, the intermediate-value theorem guarantees that f(R) = (- b, b) for some real number b and, hence, f has at least one root.
O B. Since fis a continuous function and the limits at infinity have opposite signs, the intermediate-value theorem guarantees that f(R) = R and, hence, f has at least one root.
O C. Since fis a continuous function and the limits at infinity have the same sign, the intermediate-value theorem guarantees that f(R) = [0, 00) or f(R) = (- 00, 0] and, hence, f has at least one root.
Expert Solution
Step 1 : end behaviour
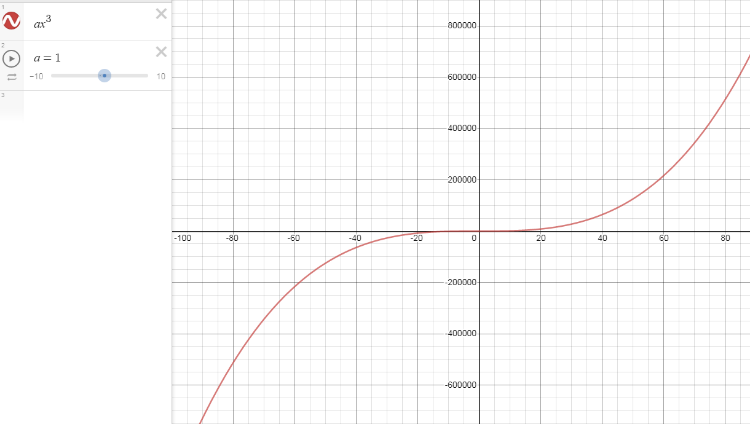
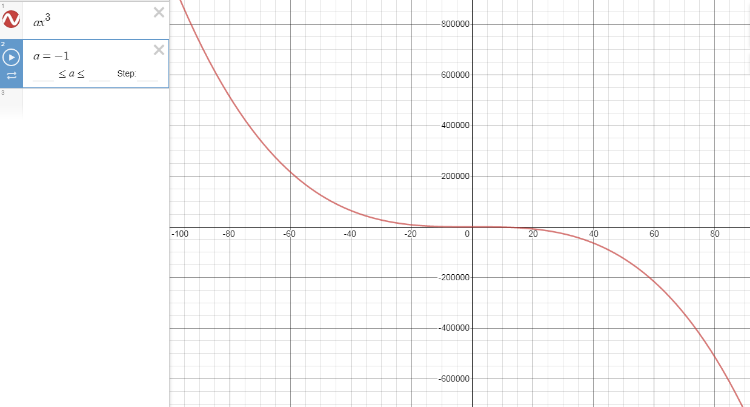
Hence option 'b' is correct.
Step by step
Solved in 2 steps with 2 images
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, advanced-math and related others by exploring similar questions and additional content below.Recommended textbooks for you
Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated
Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education
Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY
Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated
Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education
Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY
Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,
