Explain what a piecewise-defined function is and why it is used. Give an example.
Explain what a piecewise-defined function is and why it is used. Give an example.
Piecewise Function
A piecewise function is a function with multiple pieces of curves in its graph. It means it has different definitions depending upon the value of the input. i.e., a piecewise function behaves differently for different inputs.
Let us learn more about piecewise function along with how to graph it, how to evaluate it, and how to find its domain and range.
What is Piecewise Function?
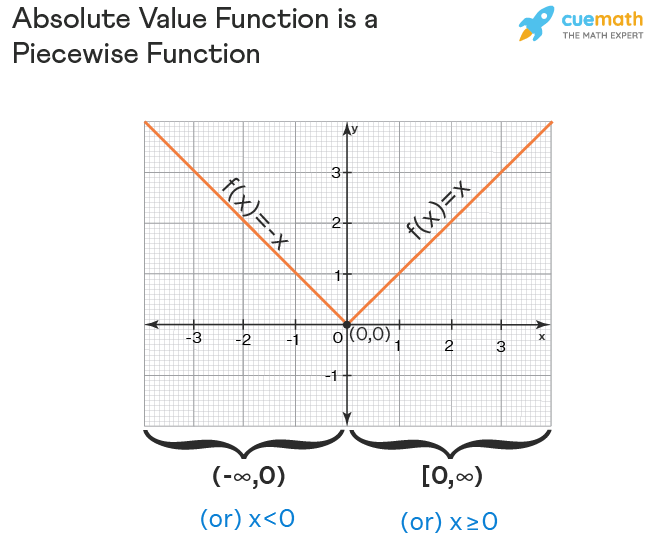
A piecewise function is a function f(x) which has different definitions in different intervals of x. The graph of a piecewise function has different pieces corresponding to each of its definitions. The absolute value function is a very good example of a piecewise function. Let us see why is it called so. We know that an absolute value function is f(x) = |x| and it is defined as:
. We should read this piecewise function as
f(x) is equal to x when x is greater than or equal to 0 and
f(x) is equal to -x when x is lesser than 0
Then the graph of absolute value function of f(x) has two pieces one corresponds to x (when x is in the interval [0, ∞) ) and the other piece corresponds to -x (when x is in the interval (-∞, 0)). Its graph looks as follows:
Step by step
Solved in 2 steps with 3 images









