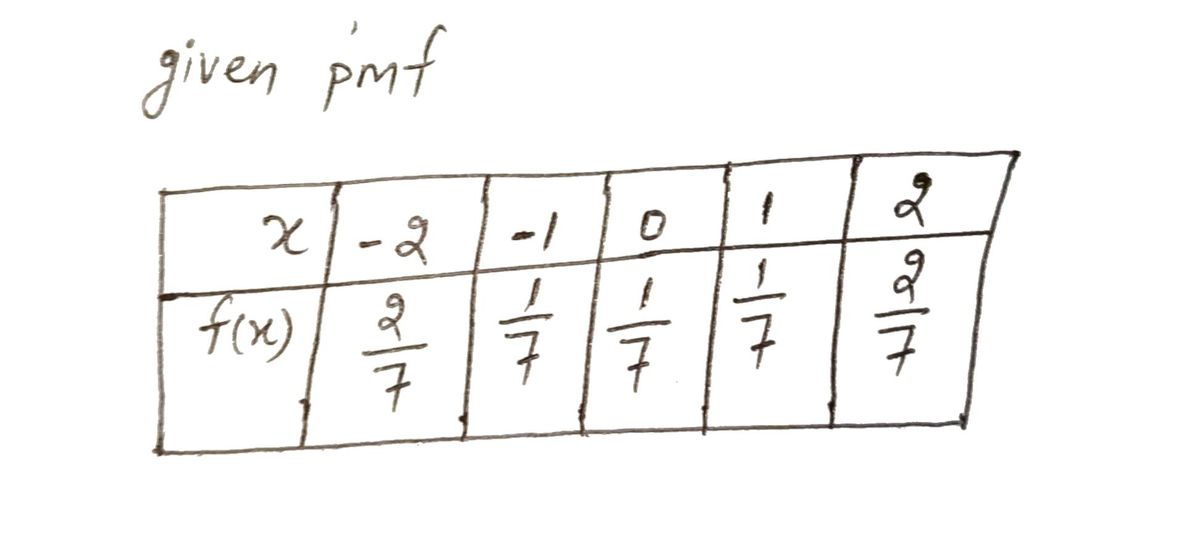
Exercise 6. Suppose a random variable has support: {−2,−1,0, 1, 2} and its pmf is: X -2 -1 0 1 2 f(x) 2/7 1/7 1/7 1/7 2/7 (a) Calculate E(X) and E(X²). (b) Using the calculated values of E(X) and E(X²) and properties of the expectation operator, calculate the following quantities: (i) E(2X – 3), (ii) E(X² – 3X), (iii) E((X− 1)²). (c) Calculate the variance of X.
Exercise 6. Suppose a random variable has support: {−2,−1,0, 1, 2} and its pmf is: X -2 -1 0 1 2 f(x) 2/7 1/7 1/7 1/7 2/7 (a) Calculate E(X) and E(X²). (b) Using the calculated values of E(X) and E(X²) and properties of the expectation operator, calculate the following quantities: (i) E(2X – 3), (ii) E(X² – 3X), (iii) E((X− 1)²). (c) Calculate the variance of X.
A First Course in Probability (10th Edition)
10th Edition
ISBN:9780134753119
Author:Sheldon Ross
Publisher:Sheldon Ross
Chapter1: Combinatorial Analysis
Section: Chapter Questions
Problem 1.1P: a. How many different 7-place license plates are possible if the first 2 places are for letters and...
Related questions
Question
![**Exercise 6.** Suppose a random variable has support: \(\{-2, -1, 0, 1, 2\}\) and its probability mass function (pmf) is:
\[
\begin{array}{c|ccccc}
x & -2 & -1 & 0 & 1 & 2 \\
\hline
f(x) & \frac{2}{7} & \frac{1}{7} & \frac{1}{7} & \frac{1}{7} & \frac{2}{7} \\
\end{array}
\]
**(a)** Calculate \(E(X)\) and \(E(X^2)\).
**(b)** Using the calculated values of \(E(X)\) and \(E(X^2)\) and properties of the expectation operator, calculate the following quantities:
(i) \(E(2X - 3)\),
(ii) \(E(X^2 - 3X)\),
(iii) \(E((X - 1)^2)\).
**(c)** Calculate the variance of \(X\).](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2Fb47fe1c9-1465-464b-a626-f1fe4168d136%2F40602638-b66c-41a3-ad2d-97ee2ca5b8bb%2F6kg3ah8_processed.png&w=3840&q=75)
Transcribed Image Text:**Exercise 6.** Suppose a random variable has support: \(\{-2, -1, 0, 1, 2\}\) and its probability mass function (pmf) is:
\[
\begin{array}{c|ccccc}
x & -2 & -1 & 0 & 1 & 2 \\
\hline
f(x) & \frac{2}{7} & \frac{1}{7} & \frac{1}{7} & \frac{1}{7} & \frac{2}{7} \\
\end{array}
\]
**(a)** Calculate \(E(X)\) and \(E(X^2)\).
**(b)** Using the calculated values of \(E(X)\) and \(E(X^2)\) and properties of the expectation operator, calculate the following quantities:
(i) \(E(2X - 3)\),
(ii) \(E(X^2 - 3X)\),
(iii) \(E((X - 1)^2)\).
**(c)** Calculate the variance of \(X\).
Expert Solution
Step 1
Step by step
Solved in 2 steps with 2 images

Recommended textbooks for you

A First Course in Probability (10th Edition)
Probability
ISBN:
9780134753119
Author:
Sheldon Ross
Publisher:
PEARSON


A First Course in Probability (10th Edition)
Probability
ISBN:
9780134753119
Author:
Sheldon Ross
Publisher:
PEARSON
