Homework Help is Here – Start Your Trial Now!
Engineering
Electrical Engineering
Exercise 1: (iii) Determine TF [g (t)]. 6) Show that TF [f (t- a)] = e -j2rva TF [f (t)] where aER *. 1) Let f be a function of the real variable t, absolutely integrable over R and continuous over a closed interval. Define the Fourier transform of this function. 7) The function (h) is defined by: h (t) = 0 if te] -0, 0 [;h (t) = t2 - t + 0.25 if te [0, 1 [; h 2) Give a physical interpretation of the Fourier transform of a function. (t) = 0 if te [1, + ∞ [. TE [f (t)] denotes the Fourier transform of a function (f). (i) Give the graphical representation of the function (h). (ii) Using the previous results, determine the Fourier transform of the function (h). 31 Show that TE [f(t)] = 2 J, f(t) cos(2nvt)dt in the case where the function (f) is End of document even. 4) Show that TE[f(t)] = -2j J. f(t) sin(2nvt) dt in the case where the function (f) is odd. 5) The function (g) is defined by: g (t) = t2.II (t), Where II (t) indicates the function 'door'. (i) Define the 'door' function. (ii) Give the graphical representation of the function (g).

Exercise 1: (iii) Determine TF [g (t)]. 6) Show that TF [f (t- a)] = e -j2rva TF [f (t)] where aER *. 1) Let f be a function of the real variable t, absolutely integrable over R and continuous over a closed interval. Define the Fourier transform of this function. 7) The function (h) is defined by: h (t) = 0 if te] -0, 0 [;h (t) = t2 - t + 0.25 if te [0, 1 [; h 2) Give a physical interpretation of the Fourier transform of a function. (t) = 0 if te [1, + ∞ [. TE [f (t)] denotes the Fourier transform of a function (f). (i) Give the graphical representation of the function (h). (ii) Using the previous results, determine the Fourier transform of the function (h). 31 Show that TE [f(t)] = 2 J, f(t) cos(2nvt)dt in the case where the function (f) is End of document even. 4) Show that TE[f(t)] = -2j J. f(t) sin(2nvt) dt in the case where the function (f) is odd. 5) The function (g) is defined by: g (t) = t2.II (t), Where II (t) indicates the function 'door'. (i) Define the 'door' function. (ii) Give the graphical representation of the function (g).

Introductory Circuit Analysis (13th Edition)
Introductory Circuit Analysis (13th Edition)
13th Edition
ISBN:9780133923605
Author:Robert L. Boylestad
Publisher:Robert L. Boylestad
Chapter1: Introduction
Section: Chapter Questions
Problem 1P: Visit your local library (at school or home) and describe the extent to which it provides literature...
See similar textbooks
icon
Related questions
Question
Can you help me only with part 7. Thanks
Exercise 1: (iii) Determine TE [g (t)]. 6) Show that TF [f (t – a)] = e -j2rva TF [f (t)] where aER *. 1) Let f be a function of the real variable t, absolutely integrable over R and continuous over a closed interval. Define the Fourier transform of this function. 7) The function (h) is defined by: h (t) = 0 if te] -∞, 0 [; h (t) = t2 - t + 0.25 if te [0, 1 [; h 2) Give a physical interpretation of the Fourier transform of a function. (t) = 0 if te [1, + ∞ [. TE [f (t)] denotes the Fourier transform of a function (f). (i) Give the graphical representation of the function (h). (ii) Using the previous results, determine the Fourier transform of the function (h). 3) Show that TF [f(t)] = 2 J, f(t) cos(2nvt)dt in the case where the function (f) is End of document even. 4) Show that TF[f(t)] = -2j J. f(t) sin(2nvt) dt in the case where the function (f) is odd. 5) The function (g) is defined by: g (t) = t2.II (t), Where II (t) indicates the function 'door'. (i) Define the 'door' function. (ii) Give the graphical representation of the function (g).
Transcribed Image Text:Exercise 1: (iii) Determine TE [g (t)]. 6) Show that TF [f (t – a)] = e -j2rva TF [f (t)] where aER *. 1) Let f be a function of the real variable t, absolutely integrable over R and continuous over a closed interval. Define the Fourier transform of this function. 7) The function (h) is defined by: h (t) = 0 if te] -∞, 0 [; h (t) = t2 - t + 0.25 if te [0, 1 [; h 2) Give a physical interpretation of the Fourier transform of a function. (t) = 0 if te [1, + ∞ [. TE [f (t)] denotes the Fourier transform of a function (f). (i) Give the graphical representation of the function (h). (ii) Using the previous results, determine the Fourier transform of the function (h). 3) Show that TF [f(t)] = 2 J, f(t) cos(2nvt)dt in the case where the function (f) is End of document even. 4) Show that TF[f(t)] = -2j J. f(t) sin(2nvt) dt in the case where the function (f) is odd. 5) The function (g) is defined by: g (t) = t2.II (t), Where II (t) indicates the function 'door'. (i) Define the 'door' function. (ii) Give the graphical representation of the function (g).
Expert Solution
Step 1

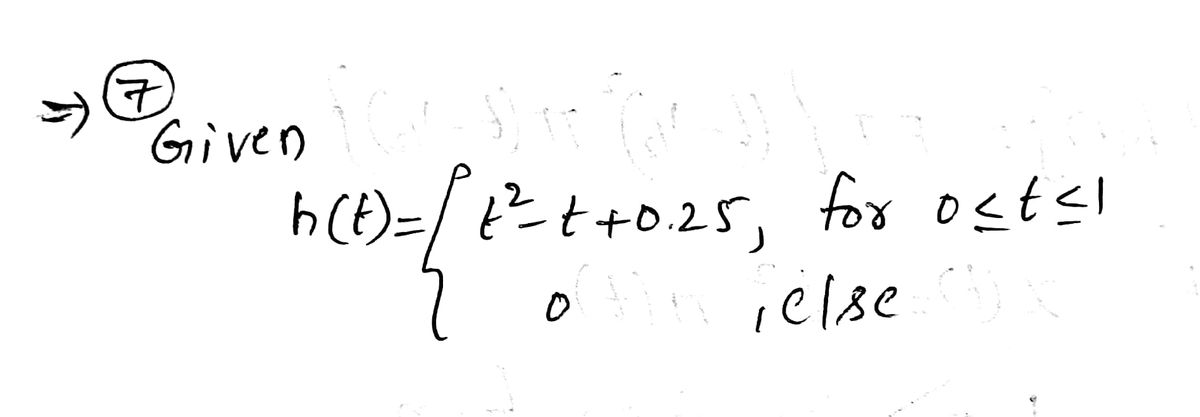
Electrical Engineering homework question answer, step 1, image 1

steps

Step by step

Solved in 5 steps with 5 images

SEE SOLUTIONCheck out a sample Q&A here
Blurred answer
Recommended textbooks for you
Introductory Circuit Analysis (13th Edition)
Introductory Circuit Analysis (13th Edition)
Electrical Engineering
ISBN:
9780133923605
Author:
Robert L. Boylestad
Publisher:
PEARSON
Delmar's Standard Textbook Of Electricity
Delmar's Standard Textbook Of Electricity
Electrical Engineering
ISBN:
9781337900348
Author:
Stephen L. Herman
Publisher:
Cengage Learning
Programmable Logic Controllers
Programmable Logic Controllers
Electrical Engineering
ISBN:
9780073373843
Author:
Frank D. Petruzella
Publisher:
McGraw-Hill Education
Fundamentals of Electric Circuits
Fundamentals of Electric Circuits
Electrical Engineering
ISBN:
9780078028229
Author:
Charles K Alexander, Matthew Sadiku
Publisher:
McGraw-Hill Education
Electric Circuits. (11th Edition)
Electric Circuits. (11th Edition)
Electrical Engineering
ISBN:
9780134746968
Author:
James W. Nilsson, Susan Riedel
Publisher:
PEARSON
Engineering Electromagnetics
Engineering Electromagnetics
Electrical Engineering
ISBN:
9780078028151
Author:
Hayt, William H. (william Hart), Jr, BUCK, John A.
Publisher:
Mcgraw-hill Education,
SEE MORE TEXTBOOKS