EXAMPLE 4 Vector Potential for a Solenoid An electric current I flowing through a solenoid (a tightly wound spiral of wire; see Figure 11) creates a magnetic field B. If we assume that the solenoid is infinitely long, with radius R and the z-axis as the central axis, then if r > R B(r) = Bk ifr < R where r = (x2 + y?)'/2 is the distance to the z-axis, and B is a constant that depends on the current strength I and the spacing of the turns of wire. (a) Show that a vector potential for B is у х RB(-.0) ifr> R A(r) = B (-y,x,0) if r < R (b) Calculate the flux of B through the surface S (with an upward-pointing normal) in Figure 11 whose boundary is a circle of radius r, where r > R. FIGURE 11 The magnetic field of a long solenoid is nearly uniform inside and weak outside. In practice, we treat the solenoid as infinitely long if it is very long in comparison with its radius.
EXAMPLE 4 Vector Potential for a Solenoid An electric current I flowing through a solenoid (a tightly wound spiral of wire; see Figure 11) creates a magnetic field B. If we assume that the solenoid is infinitely long, with radius R and the z-axis as the central axis, then if r > R B(r) = Bk ifr < R where r = (x2 + y?)'/2 is the distance to the z-axis, and B is a constant that depends on the current strength I and the spacing of the turns of wire. (a) Show that a vector potential for B is у х RB(-.0) ifr> R A(r) = B (-y,x,0) if r < R (b) Calculate the flux of B through the surface S (with an upward-pointing normal) in Figure 11 whose boundary is a circle of radius r, where r > R. FIGURE 11 The magnetic field of a long solenoid is nearly uniform inside and weak outside. In practice, we treat the solenoid as infinitely long if it is very long in comparison with its radius.
Related questions
Question

Transcribed Image Text:EXAMPLE 4 Vector Potential for a Solenoid An electric current I flowing through
a solenoid (a tightly wound spiral of wire; see Figure 11) creates a magnetic field B. If
we assume that the solenoid is infinitely long, with radius R and the z-axis as the central
axis, then
if r > R
B(r) =
Bk ifr < R
where r = (x2 + y?)'/2 is the distance to the z-axis, and B is a constant that depends on
the current strength I and the spacing of the turns of wire.
(a) Show that a vector potential for B is
у х
RB(-.0) ifr> R
A(r) =
B (-y,x,0)
if r < R

Transcribed Image Text:(b) Calculate the flux of B through the surface S (with an upward-pointing normal) in
Figure 11 whose boundary is a circle of radius r, where r > R.
FIGURE 11 The magnetic field of a long
solenoid is nearly uniform inside and weak
outside. In practice, we treat the solenoid
as infinitely long if it is very long in
comparison with its radius.
Expert Solution
Step 1
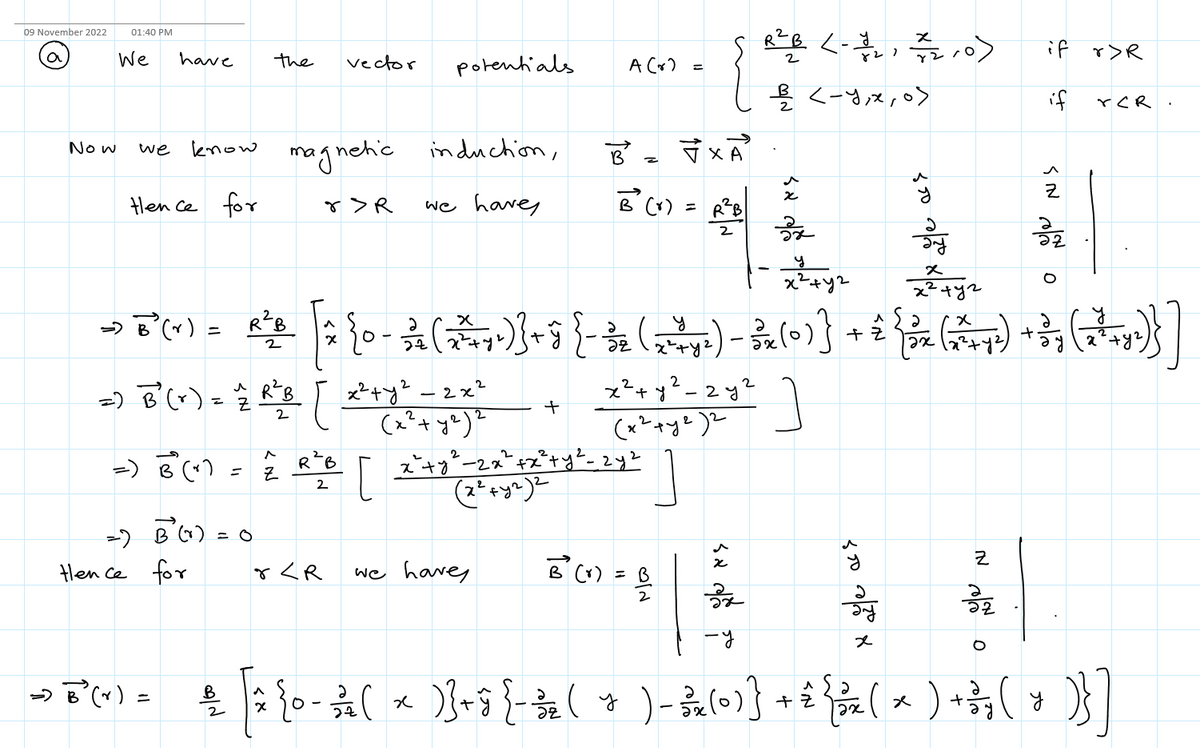
Step by step
Solved in 2 steps with 2 images
