Examine the following argument showing that the sum of the measures of the angles in any triangle is 180◦. Is the argument valid? Justify your answer. In $ABC we choose an arbitrary point D in the interior of the triangle and connect it to the three vertices of the triangle. We then mark the measures of the nine angles as shown in the figure and let the sum of the measures of the three angles in a triangle be k. We show that k = 180. Adding up all the measures of the angles in the three triangles $ABC, $ACD and $CBD we get 3k. Hence: (x+u+r)+ (v+z+t)+ (w+y+s) = 3k. By commutative and associative properties of addition we get (x+u+v+z+w+y)+ (r+t +s) = 3k. Notice that the quantity in the first parenthesis represents the sum of the measures of the angles in $ABC and for that reason equals k. This and the fact that r+t +s = 360 imply that: k+360 = 3k or k = 180.
Examine the following argument showing that the sum of the measures of the
in any triangle is 180◦. Is the argument valid? Justify your answer.
In $ABC we choose an arbitrary point D in the interior of the triangle and connect it
to the three vertices of the triangle. We then mark the measures of the nine angles as
shown in the figure and let the sum of the measures of the three angles in a triangle
be k. We show that k = 180.
Adding up all the measures of the angles in the three
$CBD we get 3k. Hence: (x+u+r)+ (v+z+t)+ (w+y+s) = 3k. By commutative
and associative properties of addition we get (x+u+v+z+w+y)+ (r+t +s) = 3k.
Notice that the quantity in the first parenthesis represents the sum of the measures of
the angles in $ABC and for that reason equals k. This and the fact that r+t +s = 360
imply that: k+360 = 3k or k = 180.

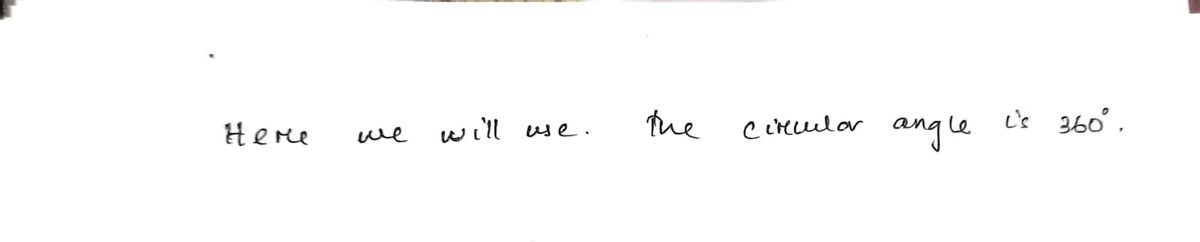
Step by step
Solved in 2 steps with 2 images




