Events A and B are such that P(A)=0.30 and P(A or B)=0.60. Given that A and B are independent and non-mutually exclusive, determine P(B).
Q: Find the probability P(E or F) if E and F are mutually exclusive, P(E)=0.34, and P(F)=0.47.
A:
Q: to agency 2. 6.91 Each of three identical jewelry boxes has two drawers. In each drawer of the first…
A: Given::- Each of three identical jewelry boxes has two drawers. In each drawer of the first box…
Q: Judy applied to ten colleges. Each college can either accept (A) or reject (R) her application.…
A: Given that: Success probability, p=0.40 Sample size, n=10
Q: A class contains 50 students. The probability of failing in one of the courses for each : 0.035, but…
A: From the given information, There are 50 students. The probability of failing in one of the courses…
Q: Find the probability of at least 2 female visitors in 17 visitors to Mt. Rainier National Park.…
A: The provided information are: Probability of success (p) = 0.5 Number of trials (n) = 17
Q: By rewriting the formula for the Multiplication Rule, you can write a formula for finding P(A and B)…
A: Let A denote the probability that a flight departs on time and B denote the probability that a…
Q: Find the probability P(E or F) if E and F are mutually exclusive, P(E)=0.41, and P(F)=0.51.…
A: Given that,P(E) = 0.41P(F) = 0.51E and F are mutually exclusive events.
Q: (a) the probability of transmitting (1) with condition of receiving (1) at the receiver end. (b) the…
A: Given, P(m1) = 0.45 So, P(m0) = 1-0.45 = 0.55 P(B0|m0) = 0.40, So, P(B1|m0) = 1-0.4 =0.60 P(B0|m1)…
Q: Q.2 the probability that a missile hit the target is 0.90. If three missile of this type has been…
A: let X be the hit the target n=3, p=0.90 X~B(3,0.90) (1) P(X>=2)= ? (2) P(X=2)= ?
Q: By rewriting the formula for the Multiplication Rule, you can write a formula for finding P(A and B)…
A:
Q: Let A and B be events with P(A) = ½ , P(B) = 1/3, and P(AUB) = 7/12. Find (P(A∩B) Select one: a.…
A: Given P(A) =1/2 , P(B) = 1/3, and P(AUB) = 7/12. Find (P(A∩B)= ?
Q: The instructor of a discrete mathematics class gave two tests. Forty percent of the students…
A: It is known that x is xy×100% of y and y is yx×100% of x.
Q: Find the probability of at least 2 female visitors in 19 visitors to Mt. Rainier National Park.…
A: Given that male and female visitors are equally likely. That is, P(male)=P(female)=1/2=0.5 Let us…
Q: n a ten day period, the probability of a certain number of outbreaks of a contagious viral infection…
A: X01234P(X)0.300.400.270.020.01
Q: Use the table to find the probabilities for a juice chosen from the shelf at random. P(less than…
A:
Q: Variable X assumes 0, 1, 2 and 3 with probabilities 0.3, a, 0.1, and b, respectively. Find a and b…
A:
Q: By rewriting the formula for the multiplication rule, you can write a formula for finding…
A: Let A - airplane flight departs on time B - flight arrives on time Given that, P(A) = 0.89 P(B) =…
Q: By rewriting the formula for the multiplication rule, you can write a formula for finding…
A:
Q: Let Pi denote the probability of getting a disease if vaccinated, and P2 denotes the probability of…
A: Let, p1 denotes the probability of getting the disease if vaccinated. p2 denotes the probability of…
Q: The probability that a man develops some form of cancer in his lifetime is 0.4567. The probability…
A: The probability that a man develops cancer in his lifetime is .The probability that a man has at…
Q: Construct a figure where the first outcome is one of X,Y, and Z, and the second outcome in each case…
A: The figure showing first outcome to be one of the X, Y, and Z and second case in each case is one of…
Q: A shooter has 4 bullets. He shoots at the target until he hits it for the first time . And stop…
A: Given that, a shooter has 4 bullets. He shoots at the target until he hits it for the first time and…
Q: 5. Let P be a probability measure and A, B two events. Show that |P(An B) – P(A)P(B)| < . Hìnt: Show…
A:
Q: A class contains 30 students. The probability of failing in one of the courses for each student is…
A: Given information: The number of students is n = 30. The probability of failing in one of the…
Q: selected person is a runner (the event R) is P(R) = 0.2. The probability that a randomly selected…
A:
Q: Let X and Y be two possible events with P(X) = 0.3 and P(Y) = 0.20 respectively. Assume that events…
A: The two probability values are P(X) =0.3 and P(Y)=0.20
Q: By rewriting the formula for the Multiplication Rule, you can write a formula for finding…
A: Let A - airplane flight departs on time B - flight arrives on time Given that, P(A) = 0.92 P(B) =…
Q: Determine whether the alternate hypothesis is left-tailed, right-tailed, or two-tailed. Ho:= 49…
A: According to the given information, we have Null and alternative hypothesis are given. Null…
Q: A college finds that 58% of students have taken a distance learning class and that 68% of students…
A: Given that, 58% of students have taken a distance learning class 68% of students are part time…
Q: gold watch? 692 In a factory manufacturing fountain pens, machines X, Y and Z manufacture 20, 30 and…
A: Given that,In a factory manufacturing fountain pens, machines X, Y and Z manufacture 20, 30 and 50…
Q: Let x = time spent waiting in a doctor’s office. Which of the following statements is false?…
A: given that X is the time spent waiting in the doctor's office.
Q: Use the information below to find the probability that a flight arrives on time given that it…
A: Let the event D be the airplane flight departs on time, and A be the airplane flight arrives on…
Q: < 400ml 2 400ml total Low sugar available No low sugar 45 35 80 15 105 120 Total 60 140 200
A: We use the given contingency table to find the required probability.
Q: E, F are independent events. P(E) = 0.2, P(F) = 0.3. Find P(E ∪ F).
A: From the provided information, P (E) = 0.2 P (F) = 0.3 The events are independent.
Q: Find the probability P(E or F) if E and F are mutually exclusive, P(E)=0.34, and P(F)=0.51. The…
A: Solution: Given information: IF E and F are mutually exclusive events then P( E∩F)=0 P( E)= 0.34 P(…
Q: Nine independent machines are used in an operation where the probability of a machine to function is…
A: From the provided information, Sample size (n) = 9 Probability of success (p) = 0.95 The process…
Q: By rewriting the formula for the multiplication rule, you can write a formula for finding P(A and B)…
A: It is given that the probability that an airline flight departs on time is 0.91, the probability…
Q: A class contains 50 students. The probability of failing in one of the courses for each student is…
A: From the given information, There are 50 students. The probability of failing in one of the courses…
Q: Q20. If a number x is chosen at random from the numbers -2,-1,0,1,2. Then, the probability that x²<2…
A:
Q: By rewriting the formula for the Multiplication Rule, you can write a formula for finding…
A: Answer: - Given, the probability that an airplane flight departs on time is P(A) = 0.91…
Q: Find the probability P(E or F) if E and F are mutually exclusive, P(E) = 0.25, and P(F0.45. The…
A: Two events say E and F are said to mutually exclusive if there exists not a single outcome that is…
Q: Compute the probability that p is less than 0.37.
A: n = 600 p̂ = 0.33
Q: Suppose that E and F are two events and that P(E)=0.8 and P(F|E)=0.5. What is P(E and F)?
A: Given data, P(E)=0.8 P(F|E)=0.5 P(E and F)=?
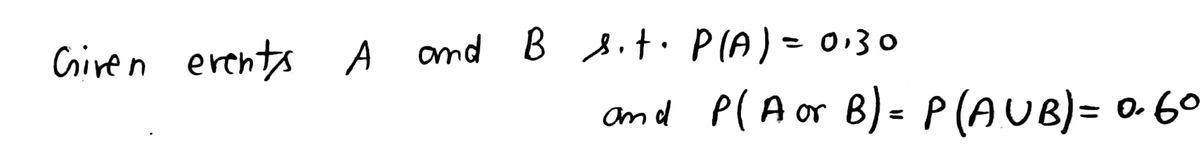
Step by step
Solved in 2 steps with 2 images
- A class contains 30 students. The probability of failing in one of the courses for each student is 0.02, but there is no chance to fail in more than one course. You know that a student failed in a course, the probability that the fail reason in non-attendance is 0.015. All other fail reasons are low average. The examinations are private, so the results are mutually independent. Let X and Y be the numbers of failed students due to non-attendance and due to low average, respectively, in that class this semester. Find the joint MGFA bag contains 4 Blue balls, 7 Red balls, and 8 Green balls. Two balls are going to be drawn from the bag (one at a time) and then put to the side (they are not returned to the bag). Let event B = blue ball chosen, R = Red ball chosen, and G- Green ball chosen. What is P(BR)? Write an answer to 4 decimal places.Consider the following statement: The probability that Mary (spends at least, spends at most, spends less than, spends more than) 20 minutes per day exercising. Depending on which phrase you chose in parenthesis you end up with a different expression and meaning in terms of probability theory. For instance, P ( x ≤ 20 )(probability Mary spends at most 20 minutes exercising) means something different from P ( x > 20 )(probability Mary spends more than 20 minutes exercising). Write an expression related to your major for each of phrases above and label them with the correct mathematical symbol (use my example as a reference, but I encourage creativity here!). Then explain the differences between the four statements i.e., differences between at least, at most, less than, more than.
- A commuter must pass through three traffic lights on her way to work. For each traffic light, the probability that it is green when she arrives is 0.6. The lights are independent. 3 (a) Compute the probability that all three lights are green. (b) The commuter goes to work five days per week. Let X be the number of times out of the five days in a given week that all three lights are green. Assume the days are independent of one another. Determine the distribution of X. (c) Calculate P(X= 3).A class contains 40 students. The probability of failing in one of the courses for each student is 0.03, but there is no chance to fail in more than one course. You know that a student failed in a course, the probability that the fail reason in non-attendance is 0.04. All other fail reasons are low average. The examinations are private, so the results are mutually independent. Let X and Y be the numbers of failed students due to non-attendance and due to low average, respectively, in that class this semester. Find the joint MGFneed it urgently please
- Q2: Two numbers x and y are selected at random between zero and one. Let the events A, B, and C be defined as follows: A = (x > 0.6), B = (y > 0.2), and C = (x > 2y). Are the events A and B independent? Are A and C independent?A bag contains 9 Blue balls, 5 Red balls, and 7 Green balls. Two balls are going to be drawn from the bag (one at a time) and then put to the side (they are not returned to the bag). Let event B = blue ball chosen, R = Red ball chosen, and G = Green ball chosen. What is P(BR)? Write an answer to 4 decimal places. IhBy rewriting the formula for the multiplication rule, you can write a formula for finding conditional probabilities. The conditional probability of event B occurring, given that event A has occurred, is P(B A)=P(A and B)P(A). Use the information below to find the probability that a flight departed on time given that it arrives on time. The probability that an airplane flight departs on time is 0.89. The probability that a flight arrives on time is 0.89. The probability that a flight departs and arrives on time is 0.82. The probability that a flight departed on time given that it arrives on time is ____ (Round to the nearest thousandth as needed.)
- By rewnting the formula for the multiplication rule, you can write a formula for finding P(A and B) P(A) conditional probabilities. The conditional probability of event B occurring, given that event A has occurred, is P(B A)= Use the information below to find the probability that a flight departed on time given that it arrives on time. The probability that an airplane flight departs on time is 0.91. The probability that a flight arrives on time is 0.89. The probability that a flight departs and arrives on time is 0.82. The probability that a flight departed on time given that it arrives on time is. (Round to the nearest thousandth as needed.) esAssume that a researcher randomly Probabilities of Girls O selects 14 newborn babies and counts the number of girls selected x. The probabilities corresponding to the 14 possible values of x are summarized in the given table. x(girls) P(x) x(girls) P(x) x(girls) P(x) 0 0.000 5 0.122 10 0.061 1 0.001 6 0.183 11 0.022 20.006 70.209 12 0.006 Find the probability of selecting 9 or more girls. 3 0.022 80.183 13 0.001 4 0.061 90.122 14 0.000 ОА. 0.122 О В. 0.061 ОС. 0.212 O D. 0.001 Click to select your answer.Use the information that, for events A and B, we have P(A) = 0.3, P(B) = 0.4, and P(A and B) = 0.1. Find P(not B). Enter the exact answer. P(not B) = i eTextbook and Media
